Question 1156643: Find the values of a, b, and c so that (ax^2+bx+c)(4x−1) = −12x^3+11x^2+18x−5
I honestly do not know where to start with this.
I try to factor but I do not think it works.
Found 4 solutions by josgarithmetic, ikleyn, MathTherapy, greenestamps:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Use polynomial division to find the quadratic expression and then identify corresponding coefficients.
That division process (not shown ) should give quotient of 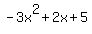 . .
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
MAKE FOIL and THEN COMPARE the coefficients.
Start comparing from the highest degree, and then go in descending order.
Do not use polynomial division, as the other tutor instructs you.
It is the way to NOWHERE.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I don't know why tutor @ikleyn says polynomial division leads you nowhere. That is simply not true; it is a perfectly good method for solving the problem.
But it is clumsy, and hard for most people to do.
You could also use synthetic division. Synthetic division is for dividing a polynomial by x-a; since here the divisor is 4x-1, you can divide by x-1/4 and divide the answer you get by 4:
1/4 | -12 11 18 -5
|
-------------------
-12
1/4 | -12 11 18 -5
| -3
-------------------
-12 8
1/4 | -12 11 18 -5
| -3 2
-------------------
-12 8 20
1/4 | -12 11 18 -5
| -3 2 5
-------------------
-12 8 20 0
When dividing by (x-1/4) the quotient is 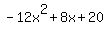 ; so when dividing by 4x-1 the quotient is ; so when dividing by 4x-1 the quotient is 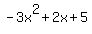 . .
However, for most people, synthetic division is not the fastest way to solve the problem.
In some form or another, performing the multiplication of polynomials on the left and comparing coefficients is usually faster.
Tutor @MathTherapy has shown the complete process in detail. But you can get to the answer with less work than he shows.
(1) In the polynomial multiplication, the only place we get an x^3 term is from the product of the leading terms:

Since the x^3 term in the product is 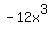 , we know , we know


(2) Similarly, in the multiplication, the only place we get a constant term is from the product of the two constants:

Since the constant term in the product is -5, we know


To find b, we can look at either the x^2 term or the x term. Suppose we choose to look at the x terms.
The x term in the product comes from 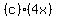 and from and from 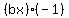 . The coefficient of the x term in the product is 18, so . The coefficient of the x term in the product is 18, so




The complete explanation of this process takes a long time and makes the process seem slow. But with a little practice it can make quick work of solving problems like this.
|
|
|