Question 1137680: Help with function homework.
Gloria is skeet shooting. The height of the skeet is modelled by the function h(t)=-4.9t^2+32t+2 where h(t) is the height in metres after t seconds. The path of Gloria’s pellet is modelled by the function g(t)=28.5t+1 , with the same units.
a) How high off the ground will the skeet be when it is hit?
b) After how many seconds will the skeet be hit?
Found 2 solutions by MathLover1, Theo:
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the height of the skeet is modeled by h(t) = -4.9t^2 + 32t + 2.
the path of gloria's pellet is modeled by g(t) = 28.5t + 1.
the skeet will be hit when h(t) = g(t).
it's easy to find using the desmos.com calculator.
here's what that calculator shows me.
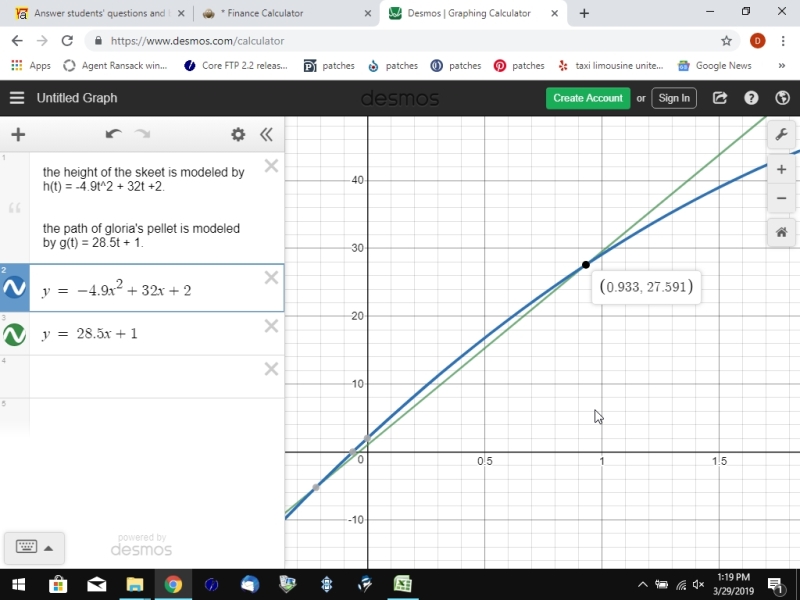
the calculator says that the bullet and the skeet will meet in .933 seconds after the gun has been fired and the skeet has been launched.
based on the formulas, the gun was fired and the skeet was launched at the same time.
also based on the formulas, the skeet was launched at a height of 2 meters and the gun was fired at a height of 1 meter.
those are the y-intercepts of the grass: the value of y when the value of x is 0.
for graphing, i replaced h(t) and g(t) with y and i replaced t with x
y still represents the height of the skeet and the bullet and x still represents the seconds from when the skeet was launched and the gun was fired.
to solve algebraically, you need to find when g(t) = h(t).
to do that, you set g(t) to h(t) and solve for t.
start with h(t) = g(t) to get -4.9t^2 + 32t + 2 = 28.5t + 1.
subtract the right side of the equation from both sides of the equation to get:
-4.9t^2 + 32t + 2 - 28.5t - 1 = 0
combine like terms to get -4.9t^2 + 30.5t + 1 = 0
use the quadratic formula to get x = -.219 of .933 rounded to 3 decimal places.
this confirms the graphic solution.
the negative value of x is discarded since the number of seconds can't be negative.
the bullet and the skeet meet in .933 seconds at a height of 27.59 seconds which you find by replacing t with .933 in either equation.
if you wanted the gun to fire after the skeet was launched, then the interception point would be different.
to do that, you replace t in the equation of g(t) = 28.5t + 1, with t-k to get g(t) = 28.5 * (t-k) + 1.
that will delay the firing of the gun for k seconds and also shift the graph of the trajectory of the bullet to the right by k seconds.
for example, assume you wanted to delay the firing of the gun for 3 seconds, then the equation for the bullet would be g(t) = 28.5 * (t - 3) + 1.
graphically, that would look like this.
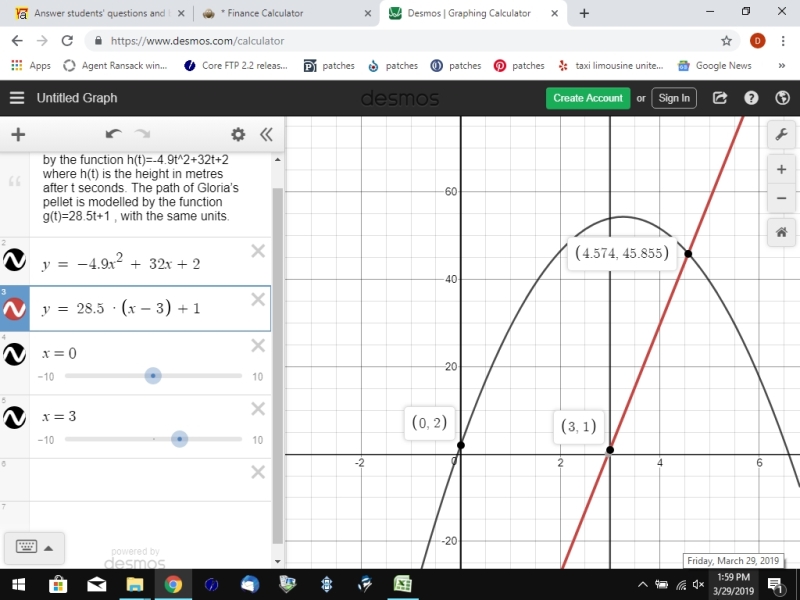
the trajectory of the bullet is the same, only it's fired off at t = 3 and the intersection point of the bullet and the skeet has changed as shown on the graph.
as before, g(t) was changed to y and t was changed to x for graphing purposes.
the solution to your questions are:
a) How high off the ground will the skeet be when it is hit?
the skeet will be hit 27.591 meters high.
b) After how many seconds will the skeet be hit?
the skeet will be hit in .933 seconds.
|
|
|