Question 1137592: Please help with this question.
The demand function for a new DVD is p(x)=-2.5x+17.5 where p(x) represents the selling price, in thousands of dollars, and x is the number of DVDs sold, in thousands.
a) Determine the revenue function.
b) Determine the maximum revenue.
c) Determine the number of DVDs that need to be sold to reach the maximum revenue.
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 where where
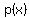 represents the selling price, in thousands of dollars, and represents the selling price, in thousands of dollars, and
 is the number of DVDs sold, in thousands. is the number of DVDs sold, in thousands.
a) Determine the revenue function.




b) Determine the maximum revenue.
 ............complete square to find ............complete square to find  , the vertex of a quadratic parabola is the highest or lowest point, the maximum or minimum , the vertex of a quadratic parabola is the highest or lowest point, the maximum or minimum


 ........ ........


the maximum is at ( , ,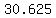 ) )
or, this way:
derivate 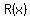 : :




find 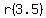 : :


 ->the ->the 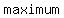 revenue revenue
c) Determine the number of DVDs that need to be sold to reach the maximum revenue.
since the maximum is at vertex ( , ,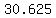 ), the number of DVDs that need to be sold to reach the maximum revenue is ), the number of DVDs that need to be sold to reach the maximum revenue is  ; so, in thousands, the number of DVDs that need to be sold to reach the maximum revenue is ; so, in thousands, the number of DVDs that need to be sold to reach the maximum revenue is 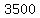
|
|
|