Question 1130918: The worlds biggest led screen is in a small mall in Bejing, China its length is ten meters more than eight times in width. the total screen area is a whooping 7,500 square meters
Found 4 solutions by Theo, greenestamps, ikleyn, josgarithmetic:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! the area of the screen is 7500 square meters.
the length is 10 meters more than eight times its width.
let L = the length and W = the width.
the formula for area of the rectangle is L * W = the area.
since the area is 7500 square meters, the formula becomes L * W = 7500
since the length is 10 meters more than eight times the width, then:
L = 8 * W + 10
the formula for area of L * W = 7500 becomes:
(8 * W + 10) * W = 7500, after your replace L with its equivalent value of 8 * W + 10
simplify (8 * W + 10) * W = 7500 to get 8 * W^2 + 10 * W = 7500
subtract 7500 from both sides of the equation to get 8 * W^2 + 10 * W - 7500 = 0
factor this quadratic equation to get W = -31.25 or W = 30
W can't be negative, so W must be equal to 30.
L = 8 * W + 10, so L = 8 * 30 + 10 = 250.
the length of the screen is 250 meters and the width of the screen is 30 meters.
the area of the screen is 250 * 30 = 7500 square meters.
solution looks good.
you could have also simplified the quadratic equation before solving to get:
8 * W^2 + 10 * W - 7500 = 0 becomes 4 * W^2 + 5 * W - 3750 = 0.
the solution would have been the same.
the problem was solved using the quadratic formula.
the width was 30.
the length was 250, which is 8 * 30 + 10.
Answer by greenestamps(13195)  (Show Source):
You can put this solution on YOUR website!
If you try to solve this problem using formal algebra, you end up having to solve the quadratic equation
Of course you can always solve a quadratic equation using the quadratic formula. But if you try to solve by factoring, there is a lot of trial and error in the process.
The problem is solved far more easily (if a formal algebraic solution is not required!) by doing the trial and error with the given information: find two numbers whose product is 7500 that satisfy the condition that one number is 10 more than 8 times the other.
We don't need to do blind guessing; we can make some useful approximations.
We can make the approximation that the longer side is 8 times the shorter side instead of 10m more than 8 times as long.
Then the approximate equation is 8x^2=7500, and we can approximate that with 8x^2=8000, or x^2=1000.
Then we can see that x should be a number close to 30.
And 30 times 250 is 7500; and 250 is 10 more than 8 times 30.
If your mental arithmetic is good, solving the problem like that is much less work than using formal algebra.
Answer by ikleyn(52752)  (Show Source):
You can put this solution on YOUR website! .
There is a way to get the solution mentally in two easy steps.
Step 1. It is clear, that the basic equation is
W*(8W + 10) = 7500.
Multiply both sides by 8:
8W*(8W+10) = 8*7500, or 8W*(2W+10) = 60000.
Step 2. What are two numbers that differ by 10 and give 60000 when multiplied ?
Look into 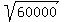 = 244.95.
Then in 5 seconds you get that the numbers are 240 and 250.
After that, you final move is
8W = 240, which implies W = 240/8 = 30.
Solved.
Answer by josgarithmetic(39613)  (Show Source):
|
|
|
