Question 1087737: Solve the quadratic inequality. Write the solution set in interval notation.Please show your complete step by step solution.
x^2+9x+13>-7
Answer by ikleyn(52779)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
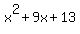 > >  ----> (add 7 to both sides) ----> ----> (add 7 to both sides) ---->
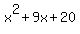 > >  ----> (factor left side) ---->
(x+5)*(x+4) > 0, or, equivalently,
(x - (-5)*(x - (-4)) > 0.
1) x < -5 ====> both factors in the left are negative; hence, the product is positive.
2) -5 < x < -4 ====> factor (x - (-5)) in the left is positive while factor (x - (-4)) in the left is positive; hence, the product is negative.
3) x > -4 ====> both factors in the left are positive; hence, the product is positive.
Answer. The solution is the union of two intervals ( ----> (factor left side) ---->
(x+5)*(x+4) > 0, or, equivalently,
(x - (-5)*(x - (-4)) > 0.
1) x < -5 ====> both factors in the left are negative; hence, the product is positive.
2) -5 < x < -4 ====> factor (x - (-5)) in the left is positive while factor (x - (-4)) in the left is positive; hence, the product is negative.
3) x > -4 ====> both factors in the left are positive; hence, the product is positive.
Answer. The solution is the union of two intervals ( , , ) U ( ) U ( , , ). ).
Solved.
If you want to learn on how to solve quadratic inequalities, read the lesson
- Solving problems on quadratic inequalities
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Inequalities".
|
|
|