SOLUTION: Solve the inequality. Write your answer in interval notation. (x + 1)/((x + 5)(x - 2)) < or = 0

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons -> SOLUTION: Solve the inequality. Write your answer in interval notation. (x + 1)/((x + 5)(x - 2)) < or = 0      Log On


   

Question 1087301: Solve the inequality. Write your answer in interval notation.
(x + 1)/((x + 5)(x - 2)) < or = 0
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
Break up the number line into regions using the critical values of the function,
x=-5
x=-1
x=2
So the four regions would be,
Region 1: 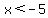x%3C-5
Region 2: 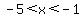-5%3Cx%3C-1
Region 3: 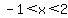-1%3Cx%3C2
Region 4: x%3E2
For each region pick a point in the region (not an endpoint) and test the inequality.
If true, it's part of the solution set.
If false, it's not part of the solution set.
The value is not important but whether it's negative or positive.
Region 1:x=-6
%28x+%2B+1%29%2F%28%28x+%2B+5%29%28x+-+2%29%29+%3C=0
%28-6%2B+1%29%2F%28%28-6+%2B+5%29%28-6+-+2%29%29+%3C=0
%28-5%29%2F%28%28-1%29%28-8%29%29%3C=0
True
Region 2:x=-2
%28x+%2B+1%29%2F%28%28x+%2B+5%29%28x+-+2%29%29+%3C=0
%28-2%2B+1%29%2F%28%28-2+%2B+5%29%28-2+-+2%29%29+%3C=0
%28-1%29%2F%28%283%29%28-4%29%29%3C=0
False
Region 3:x=0
%28x+%2B+1%29%2F%28%28x+%2B+5%29%28x+-+2%29%29+%3C=0
%281%29%2F%28%285%29%28-2%29%29+%3C=0
True
Region 4:x=3
%28x+%2B+1%29%2F%28%28x+%2B+5%29%28x+-+2%29%29+%3C=0
%283%2B+1%29%2F%28%283+%2B+5%29%283+-+2%29%29+%3C=0
%284%29%2F%28%288%29%281%29%29%3C=0
False
So then,
(-infinity,-5)U(-1,2)
Now dealing with the endpoints.
Since the inequality includes an equal sign, it's allowed as long as it doesn't make the denominator equal to zero.
In this case, x=-1 is allowed but x=-5 and x=2 are not allowed.
Designate inclusion with brackets and exclusion with parentheses.
(-infinity,-5)U[-1,2)
.
.
.
The illustration shows the regions and the solution set (where the function lies on or below the x-axis)
.
.
.