Advanced minimax problems to solve using the discriminant principle
Problem 1
Let 'x' and 'y' be nonnegative real numbers. If x^2 + y^2 = 25, then find the maximum value of x + y.
Solution
This problem can be solved using Calculus.
But I will show you how to solve it using elementary Algebra (the discriminant method).
Seeking for an elementary Algebra solution, let's introduce and add new equation
x^2 + y^2 = 25, (1)
x + y = t. (2)
Equation (1) describes a circle in the coordinate plane; equation (2) describes a straight line.
We want to find the maximum possible value of 't', when the solution to system (1), (2) does exist.
From equation (2), express y = t-x. Now substitute it into equation (1). We get
x^2 + (t-x)^2 = 25,
x^2 + t^2 - 2tx + x^2 - 25 = 0,
2x^2 - 2tx + (t^2 - 25) = 0. (3)
The value of 't' defines the position of the line in the plane: different values of 't'
produce parallel lines, and changing the value of 't' moves/translates the lines
vertically up or down, leaving them parallel.
So, they actually want you find the tangent line to the given circle with maximum value of 't',
which corresponds to the most high possible position of the tangent line.
Next, since the slope of the line is -1, from geometry intuition, it is clear that
the tangency point on the circle lies in the first quadrant.
There is another parallel tangent line to the circle, but for this second line the tangency point
is in the third quadrant.
The fact that the line (2) is the tangent line to circle (1) is equivalent to the fact that the line (2)
and the circle (1) have only one common point.
So, finding the maximum 't' is the same as finding a unique solution in 'x' of equation (3) with parameter 't'.
It described by the discriminant of quadratic equation (3)
d = b^2 - 4ac = (-2t)^2 -4*2*(t^2-25) = 0,
4t^2 - 8t^2 + 200 = 0,
-4t^2 + 200 = 0,
4t^2 = 200 --> t^2 = 200/4 = 50 --> t^2 = 50 --> t = 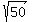 = +/-
= +/- 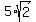 .
We are looking for the maximum value of t - so, we accept t =
.
We are looking for the maximum value of t - so, we accept t = 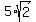 as the maximum value for t,
and reject the negative value
as the maximum value for t,
and reject the negative value 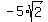 . (By the way, this negative value t=
. (By the way, this negative value t= 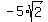 is for the other
tangent line to the circle in third quarter).
At this point, the solution to the problem is complete.
ANSWER. The maximum value of x + y is
is for the other
tangent line to the circle in third quarter).
At this point, the solution to the problem is complete.
ANSWER. The maximum value of x + y is  = +/- 6.
We are looking for the maximum value of t - so, we accept t = 6 as the maximum value for t,
and reject the negative value -6. (by the way, this negative value t= -6 is for the other
tangent line to the ellipse in third quarter).
At this point, the solution to the problem is complete.
ANSWER. The maximum value of x + y is 6.
= +/- 6.
We are looking for the maximum value of t - so, we accept t = 6 as the maximum value for t,
and reject the negative value -6. (by the way, this negative value t= -6 is for the other
tangent line to the ellipse in third quarter).
At this point, the solution to the problem is complete.
ANSWER. The maximum value of x + y is 6.
Problem 3
Find the range of function f(x) = 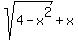 .
.
Solution
The solution to this problem can be done using Calculus.
But here I will show you how to solve it using elementary Algebra (the discriminant method).
Given function has the domain |x| <= 2, or -2 <= x <= 2.
The plot of the function is shown in the Figure below.
 Figure. Plot y =
Figure. Plot y =  + x (red line).
Blue line is the horizontal tangent line. Green line is a horizontal secant line.
As x grows starting from x = -2, the term
+ x (red line).
Blue line is the horizontal tangent line. Green line is a horizontal secant line.
As x grows starting from x = -2, the term  also grows.
So, in vicinity of x= -2, function
also grows.
So, in vicinity of x= -2, function  is the sum of two monotonic terms;
therefore, it is also monotonically risen function there.
Then it gets its maximum value between 2 and 3 in 'y' somewhere between 1 and 2 in 'x'
and starts declining. It gets the value of 2 at x= 0 and x= 2.
Our task is to find the maximum of the function. As soon as we get it, we will solve the problem.
Seeking an elementary Algebra solution, let's introduce new variable
is the sum of two monotonic terms;
therefore, it is also monotonically risen function there.
Then it gets its maximum value between 2 and 3 in 'y' somewhere between 1 and 2 in 'x'
and starts declining. It gets the value of 2 at x= 0 and x= 2.
Our task is to find the maximum of the function. As soon as we get it, we will solve the problem.
Seeking an elementary Algebra solution, let's introduce new variable
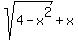 = t. (1)
Then
= t. (1)
Then
 = t-x,
4 - x^2 = (t-x)^2 <<<---=== after squaring both sides in previous equation
4 - x^2 = t^2 - 2tx + x^2,
2x^2 - 2tx + (t^2-4) = 0. (2)
Out goal is to find the maximum value of 't'.
+----------------------------------------------------------------------------------------------+
| Equation (1) and the plot in the Figure tell us that maximum value of 't' is achieved |
| when two different possible roots 'x' of equation (1) merge into one single root. |
| |
| In terms of equation (2), it means that we want to consider equation (2) as an equation |
| for 'x' with parameter 't' and want to find 't' from the condition of merging its x-roots. |
+----------------------------------------------------------------------------------------------+
It means that we want to equate the discriminant of equation (2) to zero,
considering (2) as a quadratic equation for 'x'
0 = d = b^2 - 4ac = (-2t)^2 - 4*2*(t^2-4) = 4t^2 - 8t^2 + 32 = -4t^2 + 32,
or
4t^2 = 32 --> t^2 = 32/4 = 8 --> t = +/-
= t-x,
4 - x^2 = (t-x)^2 <<<---=== after squaring both sides in previous equation
4 - x^2 = t^2 - 2tx + x^2,
2x^2 - 2tx + (t^2-4) = 0. (2)
Out goal is to find the maximum value of 't'.
+----------------------------------------------------------------------------------------------+
| Equation (1) and the plot in the Figure tell us that maximum value of 't' is achieved |
| when two different possible roots 'x' of equation (1) merge into one single root. |
| |
| In terms of equation (2), it means that we want to consider equation (2) as an equation |
| for 'x' with parameter 't' and want to find 't' from the condition of merging its x-roots. |
+----------------------------------------------------------------------------------------------+
It means that we want to equate the discriminant of equation (2) to zero,
considering (2) as a quadratic equation for 'x'
0 = d = b^2 - 4ac = (-2t)^2 - 4*2*(t^2-4) = 4t^2 - 8t^2 + 32 = -4t^2 + 32,
or
4t^2 = 32 --> t^2 = 32/4 = 8 --> t = +/-  .
The negative value for t is, obviously, irrelevant/extraneous, and we reject it.
The positive value t =
.
The negative value for t is, obviously, irrelevant/extraneous, and we reject it.
The positive value t =  gives the maximum value of the given function.
So, the range of the given function is [
gives the maximum value of the given function.
So, the range of the given function is [  ,
, ], giving the ANSWER to the problem's question.
At this point, the problem is solved completely.
], giving the ANSWER to the problem's question.
At this point, the problem is solved completely.
In this my solution, the explanation in the framed rectangle is very important.
It explains why we should interpret equation (2) as an equation relative variable x
and what form of the discriminant to use.
Problem 4
Using the discriminant method, find the range of the function y =  .
.
Solution
I will show how to solve this problem and to find the range of the given function algebraically,
using the discriminant method.
But for better understanding, I will start from the plot, which I prepared in the Figure.

Figure. Plot  .
.
Looking at the function, it is easy to see that its domain is
x^2-5 > 0, or x <  U x >
U x >  (the union of two sets).
It is consistent with the plot in the Figure.
In the area x >
(the union of two sets).
It is consistent with the plot in the Figure.
In the area x >  , when x approaches to
, when x approaches to  from the right side, the function
has vertical asymptote and asymptotically goes to infinity.
In the same area, x >
from the right side, the function
has vertical asymptote and asymptotically goes to infinity.
In the same area, x >  , when x goes to positive infinity, the function is asymptotically
close to
, when x goes to positive infinity, the function is asymptotically
close to 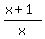 , so, it goes to 1 unit monotonically decreasing, but never achieves the value of 1.
Hence, the range of the right branch of the function at positive x >
, so, it goes to 1 unit monotonically decreasing, but never achieves the value of 1.
Hence, the range of the right branch of the function at positive x >  is from 1 to infinity,
or (
is from 1 to infinity,
or (  ,
, ).
In the area x <
).
In the area x <  , when x approaches to
, when x approaches to  from the left side, the function
has vertical asymptote and asymptotically goes to negative infinity.
In the same area, x <
from the left side, the function
has vertical asymptote and asymptotically goes to negative infinity.
In the same area, x <  , when x goes to negative infinity, the function is asymptotically
close to
, when x goes to negative infinity, the function is asymptotically
close to 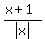 , so, it goes to negative 1 unit, or (-1), monotonically decreasing.
But at x = -3, the value of the function is (-1), as it is easy to check, and then, in the area
, so, it goes to negative 1 unit, or (-1), monotonically decreasing.
But at x = -3, the value of the function is (-1), as it is easy to check, and then, in the area
 < x < 3, the function is greater than -1 and tends to -1 from greater values than -1.
It is consistent with the plot: in the plot, you see that at
< x < 3, the function is greater than -1 and tends to -1 from greater values than -1.
It is consistent with the plot: in the plot, you see that at  < x < 3, the plot is above
the horizontal line y = -1, and tends to this asymptote y = -1, as x goes to
< x < 3, the plot is above
the horizontal line y = -1, and tends to this asymptote y = -1, as x goes to  .
Hence, the function has a local maximum somewhere between -3 and
.
Hence, the function has a local maximum somewhere between -3 and  .
+------------------------------------------------------------------------+
| The major goal of this problem is to determine this local maximum. |
| As we get this local maximum, we will solve the problem completely. |
+----------------------------------------------------------------------=-+
OK. The next part of the solution is the
.
+------------------------------------------------------------------------+
| The major goal of this problem is to determine this local maximum. |
| As we get this local maximum, we will solve the problem completely. |
+----------------------------------------------------------------------=-+
OK. The next part of the solution is the  . Let's write
. Let's write
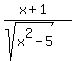 = t, (1)
by introducing new variable 't'.
We want to find maximum value of 't' in the area
= t, (1)
by introducing new variable 't'.
We want to find maximum value of 't' in the area  < x <
< x <  .
From equation (1), we have
(x+1)^2 = t^2*(x^2-5),
x^2 + 2x + 1 = t^2*x^2 - 5t^2,
(t^2-1)x^2 - 2x - (5t^2+1) = 0. (2)
+----------------------------------------------------------------------------------------------+
| Equation (1) and the plot in the Figure tell us that maximum value of 't' is achieved |
| when two different possible roots 'x' of equation (1) merge into one single root. |
| |
| In terms of equation (2), it means that we want to consider equation (2) as an equation |
| for 'x' with parameter 't' and want to find 't' from the condition of merging its x-roots. |
+----------------------------------------------------------------------------------------------+
It means that we want to equate the discriminant d of equation (2) to zero,
considering (2) as a quadratic equation for 'x'.
So, the discriminant of equation (2) is
d = b^2 - 4ac = (-2)^2 + 4*(t^2-1)*((5t^2+1) = 4 + 4(t^2-1)*(5t^2+1).
The equation d = 0 is then
4 + 4(t^2-1)*(5t^2+1) = 0,
or
(t^2-1)*(5t^2+1) = -1. (3)
For simplicity, let's introduce new variable u = t^2.
Then equation (3) takes the form
(u-1)*(5u+1) = -1,
5u^2 - 4u - 1 = -1,
5u^2 - 4u = 0,
u*(5u - 4) = 0.
It has the roots u = 0 and u =
.
From equation (1), we have
(x+1)^2 = t^2*(x^2-5),
x^2 + 2x + 1 = t^2*x^2 - 5t^2,
(t^2-1)x^2 - 2x - (5t^2+1) = 0. (2)
+----------------------------------------------------------------------------------------------+
| Equation (1) and the plot in the Figure tell us that maximum value of 't' is achieved |
| when two different possible roots 'x' of equation (1) merge into one single root. |
| |
| In terms of equation (2), it means that we want to consider equation (2) as an equation |
| for 'x' with parameter 't' and want to find 't' from the condition of merging its x-roots. |
+----------------------------------------------------------------------------------------------+
It means that we want to equate the discriminant d of equation (2) to zero,
considering (2) as a quadratic equation for 'x'.
So, the discriminant of equation (2) is
d = b^2 - 4ac = (-2)^2 + 4*(t^2-1)*((5t^2+1) = 4 + 4(t^2-1)*(5t^2+1).
The equation d = 0 is then
4 + 4(t^2-1)*(5t^2+1) = 0,
or
(t^2-1)*(5t^2+1) = -1. (3)
For simplicity, let's introduce new variable u = t^2.
Then equation (3) takes the form
(u-1)*(5u+1) = -1,
5u^2 - 4u - 1 = -1,
5u^2 - 4u = 0,
u*(5u - 4) = 0.
It has the roots u = 0 and u =  = 0.8.
The root u = 0 is irrelevant and we reject it.
The root u = 4/5 = 0.8 gives us
t^2 = = 0.8, t = +/-
= 0.8.
The root u = 0 is irrelevant and we reject it.
The root u = 4/5 = 0.8 gives us
t^2 = = 0.8, t = +/- 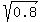 = +/-
= +/- 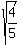 = +/-
= +/- 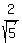 = +/- 0.894427.
The positive value is irrelevant (extraneous), and we reject it.
But the negative value, t = -0.894427 gives us the maximum value of the function y =
= +/- 0.894427.
The positive value is irrelevant (extraneous), and we reject it.
But the negative value, t = -0.894427 gives us the maximum value of the function y = 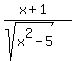 for its left branch over the domain
for its left branch over the domain  < x < -3.
Thus the range of the given function is (
< x < -3.
Thus the range of the given function is (  ,
,  ] U (
] U ( 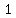 ,
, ),
the union of two intervals.
It is consistent with my plot at the beginning of the solution.
At this point, the problem is solved completely.
),
the union of two intervals.
It is consistent with my plot at the beginning of the solution.
At this point, the problem is solved completely.
In this my solution, the explanation in the framed rectangle is very important.
It explains why we should interpret equation (2) as an equation relative variable x
and what form of the discriminant to use.
My other lessons on quadratic equations in this website are
- Introduction into Quadratic Equations
- PROOF of quadratic formula by completing the square
- HOW TO complete the square - Learning by examples
- HOW TO solve quadratic equation by completing the square - Learning by examples
- Solving quadratic equations without quadratic formula
- Who is who in quadratic equations
- Using Vieta's theorem to solve quadratic equations and related problems
- Find a number using quadratic equations
- Find an equation of the parabola passing through given points
- Problems on quadratic equations to solve them using discriminant
- Relative position of a straight line and a parabola on a coordinate plane
- Using quadratic equations to solve word problems
- Word problems on engineering constructions of parabolic shapes
- Challenging word problems solved using quadratic equations
- Business-related problems to solve them using quadratic equations
- Rare beauty investment problem to solve using quadratic equation
- HOW TO solve the problem on quadratic equation mentally and avoid boring calculations
- Entertainment problems on quadratic equations
- Prime quadratic polynomials with real coefficients
- Problem on a projectile moving vertically up and down
- Problem on an arrow shot vertically upward
- Problem on a ball thrown vertically up from the top of a tower
- Problem on a toy rocket launched vertically up from a tall platform
- Problems on the area and the dimensions of a rectangle
- Problems on the area and the dimensions of a rectangle surrounded by a strip
- Problems on a circular pool and a walkway around it
- OVERVIEW of lessons on solving quadratic equations
Use this file/link ALGEBRA-I - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-I.

