SOLUTION: The solve and graph the solution set (x +2)(x-20)(x+1)>0 {x|_}

Algebra ->  Quadratic Equations and Parabolas -> SOLUTION: The solve and graph the solution set (x +2)(x-20)(x+1)>0 {x|_}      Log On


   

Question 470988: The solve and graph the solution set (x +2)(x-20)(x+1)>0 {x|_}
Found 2 solutions by jim_thompson5910, lwsshak3:
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Solving 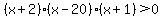%28x%2B2%29%28x-20%29%28x%2B1%29%3E0


First, find the zeros of y=%28x%2B2%29%28x-20%29%28x%2B1%29.


%28x%2B2%29%28x-20%29%28x%2B1%29=0.


x%2B2=0 or x-20=0 or x%2B1=0.


x=-2 or x=20 or x=-1.


In ascending order, the zeros are: -2, -1, 20


So this means we have the following intervals to check: , , ,


Now in the interval , the expresssion %28x%2B2%29%28x-20%29%28x%2B1%29 is negative. Simply plug in any number less than -2 to see this (eg: plug in x=-3 to get (-3+2)*(-3-20)*(-3+1)=-46)


In the interval , the expresssion %28x%2B2%29%28x-20%29%28x%2B1%29 is positive. Simply plug in any number between -2 and -1 to see this (eg: plug in x=-1.5 to get (-1.5+2)*(-1.5-20)*(-1.5+1)=5.375)


In the interval , the expresssion %28x%2B2%29%28x-20%29%28x%2B1%29 is negative. Simply plug in any number between -1 and 20 to see this (eg: plug in x=10 to get (10+2)*(10-20)*(10+1)=-1320)


Finally, in the interval , the expresssion %28x%2B2%29%28x-20%29%28x%2B1%29 is positive. Simply plug in any number greater than 20 to see this (eg: plug in x=21 to get (21+2)*(21-20)*(21+1)=506)


So the following intervals yield positive outputs: and


-----------------------------------------------


Answer:


The solution set is


Here's a graph to visually confirm this




Answer by lwsshak3(11628) About Me  (Show Source):
You can put this solution on YOUR website!
The solve and graph the solution set (x +2)(x-20)(x+1)>0
**
f(x)= (x +2)(x-20)(x+1)>0
Draw a number line with zeros on it:
-∞..........-2.......... -1...........20..........∞ (zeros on number line)
-∞.....-.....0......+.....0.....-......0....+.....∞ (sign of (f(x))
Solution is to find the sign of f(x) within intervals between zeros on the number line.
Here is the procedure:
Starting from the right side,
For x>20, f(x)>0
For -1 < x< 20, f(x)<0
For -2 < x< -1, f(x)>0
For -2 < x< -1, f(x)<0
For -∞ < x< -2, f(x)>0
You can notice that the sign switches every time we go thru a zero. This happens when the zero is an odd multiplicity (1, 3. 5, etc) Since zeros are of multiplicity 1, sign of f(x) switches every time we go thru a zero. When zeros are of even mulltiplicity (2, 4, 6, etc),The sign of f(x) does not change as we go thru the zero on the number line. Once you have the correct number line showing signs of f(x), you have the solution.
..
For given problem:
solution:(-2,-1) U (20,∞)