Question 265881: Sue rowed her boat across Lake Bend and back in 3 hours. If her rate returning was 2 mph less than the rate going, and if the distance each way was 7 miles, find her rate going.
I am having a hard time setting up this problem.
Found 2 solutions by mananth, Edwin McCravy:
Answer by mananth(16946)   (Show Source):
You can put this solution on YOUR website! Sue rowed her boat across Lake Bend and back in 3 hours. If her rate returning was 2 mph less than the rate going, and if the distance each way was 7 miles, find her rate going.
let her going rate be x
her returnibg rate was x-2
Time taken while going + time taken while returning = 3 hours
7/x + 7/ x-2 = 3
solve the equation to get the speed
Answer by Edwin McCravy(20060)  (Show Source):
You can put this solution on YOUR website! Sue rowed her boat across Lake Bend and back in 3 hours. If her rate returning was 2 mph less than the rate going, and if the distance each way was 7 miles, find her rate going.
Let R=the rate going
Make this chart:
Distance Rate Time
Going
Returning
Fill in the two distances which is given as 7 each:
Fill in R for the rate going:
Distance Rate Time
Going 7 R
Returning 7
We are told that her rate returning was 2 mph less than
her rate going, so subtract 2 from R, getting R-2, and
fill that in for her rate returning:
Distance Rate Time
Going 7 R
Returning 7 R-2
Now we use the fact that 
to fill in the two TIMES:
Distance Rate Time
Going 7 R 7/R
Returning 7 R-2 7/(R-2)
We are told that she rowed her boat across Lake Bend and
back in 3 hours, so we make our equation from that by
adding the two times and setting that equal to 3 hours.
Multiply by the LCD of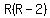 
That doesn't factor so we have to use the quadratic
formula:
with  ,  ,  , 
Approximating the two solutions as decimals,
R=5.871924369 and R=0.794742298
We have to discard the second answer, since that would
make her rate returning,  , a negative number.
So the answer is about 5.87 mph. going (and about 3.87 mph
returning).
Edwin
|
|
|
