Question 199939: A farmer decides to enclose a rectangle garden using one side of the barn as a side to the rectangle. What is the maximum area that the farmer can enclose with 100 ft of fence? What should the deminsons of the garden be to give this area?
Maximum area that the farmer can enclose with 100 ft of fence__________sq.ft.
Deminsons of the garden to give this area is 50 ft by __________ft.
Found 2 solutions by RAY100, ankor@dixie-net.com:
Answer by RAY100(1637)   (Show Source): (Show Source):
You can put this solution on YOUR website! Draw a rough sketch, rectangle, one side is barn, two sides are "a", and one side is"b"
.
Perimeter of new fence is 2a +b =100,,, or b=100 - 2 a
.
Lets tabulate "a" vs "b" vs Area ,,,(area = a *b )
.
a,,,,,,,,,,b,,,,,,,,,,,Area
0,,,,,,,,,,100,,,,,,,,,,,0
10,,,,,,,,80,,,,,,,,,,800
20,,,,,,,,60,,,,,,,,,1200
24,,,,,,,,52,,,,,,,,,1248
25,,,,,,,50,,,,,,,,,,1250,,,,,MAX
26,,,,,,,,,48,,,,,,,,,1248
30,,,,,,,40,,,,,,,,,,1200
40,,,,,,,20,,,,,,,,,,,,800
50,,,,,,,,0,,,,,,,,,,,,,,,,0
.
Max Area is 1250 sq ft,,,,with dim of 25 by 50 , (50 opposite barn side)
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A farmer decides to enclose a rectangle garden using one side of the barn as
a side to the rectangle. What is the maximum area that the farmer can enclose
with 100 ft of fence? What should the dimensions of the garden be to give this area?
Maximum area that the farmer can enclose with 100 ft of fence__________sq.ft.
:
Let x = the width of the garden
Let L = the length
:
The perimeter equation for 3 sides:
L + 2x = 100
L = (100-2x)
:
The area equation:
A = x * L
Replace L with (100-2x)
A = x(100-2x)
A = -2x^2 + 100x
:
Find the axis of symmetry of this quadratic equation a=-2; b=100
x = 
x = 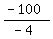
x = +25 ft is the width for max area
:
L = 100 - 2(25)
L = 50 ft
:
Max area: 50 * 25 = 1250 sq/ft
|
|
|