Question 161461: I don't have any idea how to do these word problems. I've been trying but I just don't get it. Can you please help me? I can never understand word problems.
1) The distance an object falls is directly proportional to the square of the time it has been falling. After 6 seconds it has fallen 1296 feet. How longwill it take to fall 2304 feet?
2) x varies directly as the square of s and inversely as t. How does x change when s is doubled? When both s and t are doubled?
If you can help I'd really appreciate it. Thank you so much! I could not do this without you.
Found 2 solutions by KnightOwlTutor, MathTherapy:
Answer by KnightOwlTutor(293)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. distance= aXtime squared. we know that distance is proportinal but we don't know what a is. That is why they gave you the time and the distance in the first part of the equation. This will solve for the unknown a so that you can proceed to the second part of the problem.
1296=a(6)^2 1296=36a
divide both sides by 36
a=12
We have the distance and a so we can solve for t
2304=12(t)^2
Divide both sides by 12
192=t^2
Take the square root
t=13.85 seconds
Let's check by plugging into the equation to see if we are right
12(13.9)^2=2,318.52
It is a close approximation for the problem.
2) x varies directly as the square of s and inversely as t. How does x change when s is doubled? When both s and t are doubled?
x=s^2/t We know that when something varies directly. it is like this a=b
When something varies indirectly it looks like this a=1/b
when s is doubled
x=(2s)^2/t x=4s^2/t x is 4x as great.
When both s and t are doubled
x=(2S)^2/2t= x=4s^2/2t x=2s^2/t the value x is doubled
Answer by MathTherapy(10575)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I don't have any idea how to do these word problems. I've been trying but I just don't get it. Can you please help me?
I can never understand word problems.
1) The distance an object falls is directly proportional to the square of the time it has been falling. After 6 seconds
it has fallen 1296 feet. How longwill it take to fall 2304 feet?
2) x varies directly as the square of s and inversely as t. How does x change when s is doubled? When both s and t are doubled?
If you can help I'd really appreciate it. Thank you so much! I could not do this without you.
1) The distance an object falls is directly proportional to the square of the time it has been falling.
After 6 seconds, it has fallen 1296 feet. How long will it take to fall 2304 feet?
D = 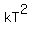 1,296 =
1,296 = 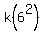 ----- Substituting 1,296 for D (distance), and 6 for T (time)
1,296 = 36k ----- Substituting 1,296 for D (distance), and 6 for T (time)
1,296 = 36k
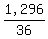 = k
36 = k
D = = k
36 = k
D = 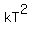 2,304 =
2,304 = 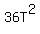 --- Substituting 2,304 for D (distance), and 36 for k --- Substituting 2,304 for D (distance), and 36 for k
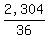 = =  64 =
64 =  Time taken by object to fall 2,304 feet, or
Time taken by object to fall 2,304 feet, or  = 8 secs
====================================
2) x varies directly as the square of s and inversely as t. How does x change when s is doubled?
When both s and t are doubled?
2a) How does x change when s is doubled?
With this being DIRECT, and INDIRECT/INVERSE VARIATION, and with k being the CONSTANT of PROPORTIONALITY, we get the following equation:
x = = 8 secs
====================================
2) x varies directly as the square of s and inversely as t. How does x change when s is doubled?
When both s and t are doubled?
2a) How does x change when s is doubled?
With this being DIRECT, and INDIRECT/INVERSE VARIATION, and with k being the CONSTANT of PROPORTIONALITY, we get the following equation:
x = 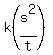 x =
x = 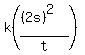 ---- Doubling s, or replacing s with 2s
x = ---- Doubling s, or replacing s with 2s
x = 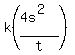 x =
x = 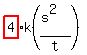 ---- Equation, after s is DOUBLED
x = ---- Equation, after s is DOUBLED
x = 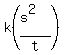 ---- ORIGINAL equation
Upon comparing the 2 equations above, it’s clearly seen that, when s is DOUBLED, x is QUADRUPLED.
======================
2b) How does x change when both s and t are doubled?
With this being DIRECT, and INDIRECT/INVERSE VARIATION, and with k being the CONSTANT of PROPORTIONALITY, we get the following equation:
x = ---- ORIGINAL equation
Upon comparing the 2 equations above, it’s clearly seen that, when s is DOUBLED, x is QUADRUPLED.
======================
2b) How does x change when both s and t are doubled?
With this being DIRECT, and INDIRECT/INVERSE VARIATION, and with k being the CONSTANT of PROPORTIONALITY, we get the following equation:
x = 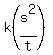 x =
x = 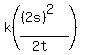 ---- Doubling “s” and “t”
x = ---- Doubling “s” and “t”
x = 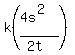 x =
x = 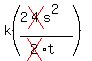 x =
x = 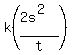 x =
x = 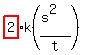 -- Equation, after “s” and “t” are DOUBLED
x = -- Equation, after “s” and “t” are DOUBLED
x = 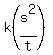 ---- ORIGINAL equation
Upon comparing the 2 equations above, it’s clearly seen that, when s and t are DOUBLED, x is DOUBLED also. ---- ORIGINAL equation
Upon comparing the 2 equations above, it’s clearly seen that, when s and t are DOUBLED, x is DOUBLED also.
|
|
|