SOLUTION: he path of a model rocket is modelled by the quadratic function h(t)=-5(t-20^+ 25, where the height, h(t),is in meters and time,t,is in seconds. a) when will the rocket reach a he

If you have the the formula for a height given to you as a function of time in the form


    h(t) = -at^2 + bt + c,    (1)


where "a", "b" and "c" are real numbers, a > 0, then in this formula



    (a)  the initial height is equal to the coefficient "c" value;


    (b)  the initial velocity is the coefficient  "b" in the formula;


    (c)  the coefficient "a" value is half of the gravity acceleration.




    (d)  To find the height at the time moment "t", simply substitute the value of "t" into the formula (1) and calculate.


    (e)  To find the time "t" when the height has a given value h = , substitute  h =  into equation (1)

         and solve equation  


             h(t) = -at^2 + bt + c = .    (2)



    (f)  To find the time when the height is maximal, use the formula


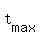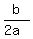              = .      (3)



    (g)  To find the maximal height, substitute the time value  t= 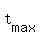  of the formula (3)  into the formula (1).