SOLUTION: Marcus states that the polynomial expression {{{3x^3-4x^2y + y^3 + 2}}} is in standard form. Ariel states that it should be {{{y^3-4x^2y+3x^3+2}}}. Explain which student is c

Click here to see ALL problems on Quadratic Equations

Question 1151789: Marcus states that the polynomial expression

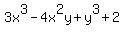
is in standard form. Ariel states that it should be
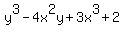. Explain which student is correct and why.
Found 3 solutions by Edwin McCravy, jim_thompson5910, ikleyn:
Answer by Edwin McCravy(20056)   (Show Source):
You can put this solution on YOUR website!

Maybe some other tutor has a different idea on this. What do you say, Ikleyn? greenestamps? josgarithmetic? jim_thompson5910? MathLover1? Marcus states that the polynomial expression 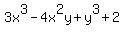is in standard form. Ariel states that it should be 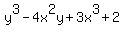. Explain which student is correct and why.
At first, I would have said both are correct. Marcus has the polynomial in descending powers of x. Ariel has put the polynomial in descending powers of y. However I think Marcus should have made the second term -4yx², not -4x²y, because each term should end with the power of the letter which the polynomial expression is in descending powers of. Edwin

Answer by jim_thompson5910(35256)   (Show Source):
You can put this solution on YOUR website!

The only difference between the polynomials Marcus and Ariel wrote out is that the and terms have been swapped.

When talking about standard form, we write the letters in alphabetical order. There is nothing inherently wrong about writing the letters out of order, but its just common convention. For example, standard form would be instead of even though they are the same expression (since we can add two numbers in any order).

A similar question is asked here
https://mymathforum.com/threads/the-letters-in-a-polynomials-standard-form.54277/

Since Marcus lists x first, then y, this means his polynomial is in standard form. Note how the exponents for x count down (from 3 to 2 to 0). The degree of any monomial is the sum of the exponents. The degrees of each mononial is counting down. The constant term is always last in any standard form polynomial.

Answer by ikleyn(52792)   (Show Source):
You can put this solution on YOUR website!
.

Standard form in this case is alphabetical ordering. It means that the outer ordering must go in descending order of total degrees of monomials. Inside the set of monomials of the same degree, the ordering should go in alphabetical ordering. It means descending order for variable x and ascending order for variable y. The opposite ordering is also admitted. But, in any case, if you talk about the standard form, you should select on EITHER direct alphabetic ordering OR opposite to the alphabetic ordering, but only ONE of the two. Mixing two different orderings in one expression is not allowed in standard form. In this sense, ordering by Marcus is CONSISTENT; the ordering by Ariel is not consistent.

--------------

Edwin, thanks for asking.

/\/\/\/\/\/\/\/

Surely, the average school Math student will not understand the reason, why this issue is discussed, at all.

It can be important for them, for example, when some problem asks them to write 24-th term of the binomial expansion of .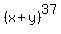

In Math, some standard ordering is also used sometimes, for example, for classification of surfaces in multi-dimensional spaces,
or when Fourier or Laplace transformations are performed on differential operators in multi-dimensional spaces,
but these subjects are far above of understanding of school students.

So, my opinion is that it is better for student to solve 25 other problems than to think / (to spend) long time on this one.