SOLUTION: Find those values of K for which x^2-kx-21=0 and x^2-3kx+35=0 have a common root.

1.  Let x and y be the two roots of the first  equation, and
    let z and y be the two roots of the second equation,  with y as a common root.


    Then, according to Vieta's theorem, you have these two equations

          x + y =  k,    (1)
          z + y = 3k.    (2)


    According to the same theorem, you also have these two equations

         xy = -21,       (3)
         yz =  35.       (4)


    Thus, we have four equations for 4 unknowns  x, y, z, and k.  Hence, it is solvable !!



2.  From (3), x = 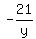.   (5)

    From (4),  z = 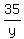    (6)


    Substitute (5) into (1). You will get 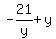 = k  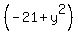====>   = ky.    (7)

    Substitute (6) into (2). You will get 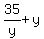 = 3k  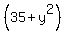====>   = 3ky.     (8)

    Divide (8) by (7).  You will get

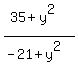            = 3  ====>  35 + y^2 = 3*(-21 + y^2)  ====>  35 + 63 = 3y^2 - y^2  ====>  2y^2 = 98  ====>  y^2 = 49  ====>  y = +/-7.


3.  Case a): y = 7.

             Then from (3)  x = -21/7 = -3  and  from (4)  y = 35/7 = 5.  Then from (1)  k = x+y = -3+5 = 2.


    Case b): y = -7.  

             Then from (3)  x = -21/(-7) = 3  and  from (4)  y = 35/(-7) = -5.  Then from (1)  k = x+y = 3-5 = -2.