Question 1088908: Consider all the points in the plane that solve the equation x^2 + 2y^2 = 16. Find the maximum value of the product xy on this graph.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  represents an ellipse centered at (0,0), represents an ellipse centered at (0,0),
which is symmetrical with respect the the x- and y-axes,
and symmetrical with respect to the origin:
 . .
There will be a maximum for 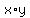 in the first quadrant, at in the first quadrant, at 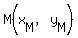 , ,
and another one at 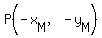 , in quadrant III. , in quadrant III.
All we have to do is find two positive numbers, the coordinates of  . .




We are looking for a value  that makes that makes  maximum. maximum.
If we say  , the expression becomes , the expression becomes  , ,
a quadratic polynomial/function:
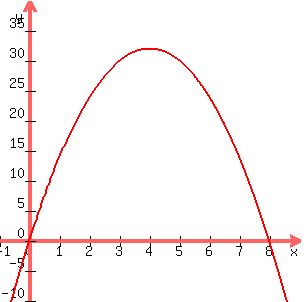 . .
If you like applying formulas (or if your teacher likes to see formulas),
you may have been told in class that
 is maximum when is maximum when 
In this case, it means that  is maximum is maximum
when  . .
Otherwise, you may realize that
 . .
That tells you that the maximum of 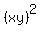 is is  , ,
meaning that the maximum of  is is  . .
If you continue working with formulas,  gives you gives you  --> -->  , ,
and  --> -->  . .
Multiplying, you get
 . .
.
|
|
|