Question 1034230: Applications of Quadratic Functions
1. The hypotenuse of a right triangle is 32 feet long. One leg is 2 feet longer than the other. Find the length of the shorter leg. Round your answer to the nearest hundredth.
2. Elaine shoots an arrow upward at a speed of 32 feet per second from a bridge that is 28 feet high. The height of the arrow is given by the function h(t) = -16t2+32t + 28, where t is the time in seconds.
a. What is the maximum height that the arrow reaches?
b. How long does it take the arrow to reach its maximum height?
c. How long would it take before the arrow reached the ground? Round your answer to the hundredths place.
3. A person standing close to the edge on the top of an 80-foot tower throws a ball with an initial speed of 64 feet per second. After t seconds, the height of the ball above the ground is
s(t) = -16t2 +64t + 80
a. After how many seconds will the ball reach its maximum height?
b. How long will it take before the ball reaches the ground?
c. What is the maximum height of the ball?
4. An object is launched at 19.6 meters per second from a 58.8 meter tall platform. The equation for the object's height s at time t seconds after launch is s(t) = -4.9t2+ 19.6t + 58.8, where s is in meters.
a. When does the object strike the ground?
b. What was its maximum height?
c. How long will it take to reach its maximum height?
5. A ball is thrown directly upward from an initial height of 200 feet with an initial velocity of 96 feet per second. After t seconds, the height of the ball above the ground is s(t) = 16t2+ 96t + 200.
a. After how many seconds will the ball reach its maximum height?
b. What was the maximum height?
c. How long will it take before the ball reaches the ground?
6. A soft-drink vendor at a popular beach analyzes his sales records, and finds that if he sells x cans of soda pop in one day, his profit (in dollars) is given by P(x) = -0.001x2+ 3x – 1800.
a. What is his maximum profit per day?
b. How many cans must be sold in order to obtain the maximum profit?
Answer by ikleyn(52778)   (Show Source):
You can put this solution on YOUR website! .
2. Elaine shoots an arrow upward at a speed of 32 feet per second from a bridge that is 28 feet high.
The height of the arrow is given by the function h(t) = -16t^2 + 32t + 28, where t is the time in seconds.
a. What is the maximum height that the arrow reaches?
b. How long does it take the arrow to reach its maximum height?
c. How long would it take before the arrow reached the ground? Round your answer to the hundredths place.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
To solve the problem, it is better to change the sequence of questions from a), b), and c) to b), a), and c). So, we start from b).
b. How long does it take the arrow to reach its maximum height?
The time "t" when the arrow reaches its maximum height is that "t" where the parabola (the quadratic function h(t) =  )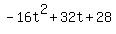
reaches the maximum. It is the parabola vertex.
From Algebra you know that this "t" is t =  =  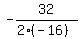= 1.
Here I refer to the formula for the vertex of the parabola of the general form h(t) =  . In your case a = -16, b = 32.
So, your answer for the time "t" is t = 1 seconds.
The arrow reaches its maximum height in 1 second.
After 1 second it will start its movement down.
So, b) is answered.
a. What is the maximum height that the arrow reaches?
Above you just found that the maximum height is reached at t = 1 seconds.
So, to find the maximum height, simply substitute t=1 into the parabola equation:
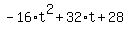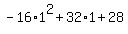 =  =  = -16 + 32 + 28 = 44.
44 feet above the ground level. It is the maximum height of the arrow.
Did I calculate it correctly? Check it please.
If "Yes", then a) is answered.
c. How long would it take before the arrow reached the ground?
The arrow reaches the ground when its height above the ground becomes zero: h(t) = 0.
It means that your quadratic function get the zero value 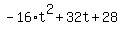 =  at that t.
So, you need to find the roots of the quadratic equation
= .
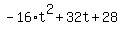Do it by applying the quadratic formula.
The quadratic formula will give you two values.
Choose the value which is positive. Only positive "t" can be the solution.
I got the value t = 3.89 (after rounding).
What is your value?
If it is the same, then the question c) is answered too and the entire problem is solved.
Do the other problems in the same manner. They all are very similar to that.
|
|
|
