Question 550989: pls.. help me in this problem.
Use the properties of proportionality to solve:
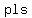 a+x+sqrt(a^2-x^2)/a+x-sqrt(a^2-x^2)=b/x a+x+sqrt(a^2-x^2)/a+x-sqrt(a^2-x^2)=b/x
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I assume your equation is

Multiplying both sides of the equal sign by the product of the denominators we get an (almost) equivalent equation stating that the cross products are equal. I assume that's what was meant by "Use the properties of proportionality."

(Multiplying by an expression that includes variables risks introducing extraneous solutions, solutions of the new equations that are not solutions of the original equation).



Now we square both sides of the equation. (By doing that we may be introducing extraneous solutions too).















 --> --> 
The expression above implies  , ensuring that the square roots in the original equation will have a real value. , ensuring that the square roots in the original equation will have a real value.
It also results in the expression  , which includes all the solutions of the original equation, plus extraneous solutions. , which includes all the solutions of the original equation, plus extraneous solutions.
If those tentative solutions were constant numbers, or simpler expressions, we could substitute and verify. In this case, it's easier to hunt down and eliminate the extraneous solutions the hard way.
Extraneous solutions include those that make the denominators zero.
There are no solutions for  or or  , which make , which make  zero. zero.
For  , the expression found for , the expression found for  turns into turns into
 , and , and  , but , but  makes a denominator in the original equation zero, so only makes a denominator in the original equation zero, so only  is a solution. is a solution.
For 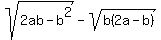 to have a real, positive value, it must be to have a real, positive value, it must be 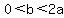 , or , or 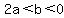 . .
However, there are solutions only if 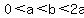 , or , or 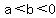 . .
For 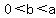  gives extraneous solutions, that make just one of the factors in gives extraneous solutions, that make just one of the factors in  negative. negative.
For 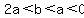 , it gives extraneous solutions that make negative exactly three of the factors in , it gives extraneous solutions that make negative exactly three of the factors in  . .
Those extraneous solutions are solutions of  that were introduced on squaring both sides. that were introduced on squaring both sides.
THE SOLUTION
 and and
 for for 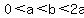 , or , or 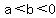
(examples: (a,b)=(5,8), (a,b)=(-5,-2)) }.
For other (a,b) pairs there are no solutions (examples: (a,b)=(-5,-8), (a,b)=(-5,-2) ).
|
|
|