Question 306292: Hi,
Thank you so much for taking my question.
If there is a ratio of 5:3 (boys to girls) at the graduation, then 12 more girls arrive, the new ratio changes to 10:9 (boys to girls). How many students are at the graduation now.
Thank you again.
Rose
Found 2 solutions by scott8148, ankor@dixie-net.com:
Answer by scott8148(6628)   (Show Source): (Show Source):
You can put this solution on YOUR website! 5k / (3k + 12) = 10 / 9
"cross" multiplying ___ 45k = 30k + 120 ___ k = 8
initially, 40 boys and 24 girls ___ finally, 40 boys and 36 girls ___ 76 students
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! If there is a ratio of 5:3 (boys to girls) at the graduation, then 12 more girls
arrive, the new ratio changes to 10:9 (boys to girls).
How many students are at the graduation now.
:
let t = total students at the grad now
:
5:3 means 5/8 are boys, 3/8 are girls
and
10:9 means 10/19 are boys, 9/19 are girls
:
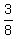 *(t - 12) + 12 = *(t - 12) + 12 = 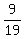 t t
multiply equation by 152 (8*19), results:
:
19*3(t-12) + 12(152) = 8*9t
57(t-12) + 1824 = 72t
57t - 684 + 1824 = 72t
1140 = 72t - 57t
1140 = 15t
t = 1140/15
t = 76 in the grad class now
:
:
see if this makes sense
76-12 = 64 originally in the class
then; 3/8(64) = 24 girls
and
9/19(76) = 36 girls, a difference of 12, confirms our solution
|
|
|