Question 1196915: Suppose a is to b as c is to d;that is, a/b =c/d
a) Show that b is to a as d is to c.
b) Show that a-b is to b as c-d is to d.
c) Show that a is to a+b as c is to c+d.
d) Show that a+b is to c+d as b is to d.
Found 2 solutions by Theo, math_tutor2020:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your are given that a/b = c/d.
multiply both sides by b and both sides by d to get:
ad = bc
(a)
start with b/a = d/c
multiply both sides by a and both sides by c to get:
bc = ad
switch sides to get:
ad = bc
this is same as you got with the given, so they're equivalent.
(b)
start with (a-b)/b = (c-d)/d
multiply both sides by b and both sides by d to get:
(a-b) * d = (c-d) * b
simplify to get:
ad - bd = cb - db
rearrange to get:
ad - bd = bc - bd
add bd to both sides to get:
ad = bc
this is the same as you got with the given so they're equivalent.
(c)
start with a/(a+b) = c/(c+d)
multiply both sides by (a+b) and both sides by (c+d) to get:
a * (c+d) = c * (a+b)
simplify to get:
ac + ad = ca + cb
rearrange to get:
ac + ad = ac + bc
subtract ac from both sides to get:
ad = bc
this is the same as you got with the given so they're equivalent.
(d)
start with (a+b)/(c+d) = b/d
multiply both sides by (c+d) and both sides by d to get:
(a+b) * d = b * (c+d)
simplify to get:
ad + bd = bc + bd
subtract bd from both sides to get:
ad = bc
this is the same as you got with the given to they're equivalent.
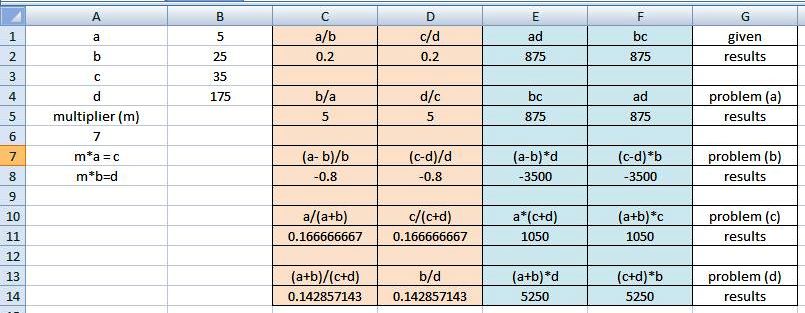
another way to show they're equivalent is to assign values to each variable so that a/b = c/d.
if i assumed that a = 5 and b = 25, then a/b = 1/5
i then multiply numerator and denominator by the same value to get another ratio.
i used 7 and got c=35 and d=175
when a = 5 and b = 25 and c = 35 and d = 175, a/b = c/d becomes 5/25 = 35/175 which becomes .2 = .2
cross multiply to get ad = bc which becomes 5*175 = 25*35 which becomes 875 = 875.
i used excel to do the calculations for the given and for problems (a) through (d).
the results from all options gave results from column C equal to results from column D and results from column E equal to results from column F.
this confirmed that all equations given in problems (a) through (d) are equivalent to results from the given equation.
here are the excel results.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Part (a)
a is to b as c is to d
a/b = c/d
ad = bc ..... multiply both sides by bd
d/c = b/a ... divide both sides by ac
b/a = d/c
b is to a as d is to c
The claim (a) is proven to be true.
We can reverse the order of 'a' vs b, as long as we reverse c and d as well.
To avoid division by zero errors, we'll have a,b,c,d as nonzero values.
-------------------------------------------------------
Part (b)
I'll start with what we want to show which is
(a-b)/b = (c-d)/d
and we'll work to reaching
a/b = c/d
In a sense, we're working backwards and we'll reverse the order later.
So,
(a-b)/b = (c-d)/d
a/b-b/b = c/d-d/d .... break up the fraction
a/b-1 = c/d-1 ....... reduce
a/b = c/d .... add 1 to both sides
Now reverse the order of the steps shown
This reversal is possible since each step can be undone, aka there's an inverse to it.
For instance, the "add 1 to both sides" step can be undone with "subtract 1 from both sides".
So this is what the steps look like when going forward
a/b = c/d
a/b-1 = c/d-1
a/b-b/b = c/d-d/d
(a-b)/b = (c-d)/d
This can be thought of as the main set of steps, while the previous paragraph is like supplementary steps or something you'd have on a separate sheet of scratch paper. Though if I was the teacher, I'd probably want to see the student's entire thought process (assuming you use this reversal method).
-------------------------------------------------------
Part (c)
Start with what we want to prove
a/(a+b) = c/(c+d)
the goal is to get to
a/b = c/d
a/(a+b) = c/(c+d)
(a+b)/a = (c+d)/c
a/a + b/a = c/c + d/c
1 + b/a = 1 + d/c
b/a = d/c
a/b = c/d
Now reverse the order to get...
a/b = c/d
b/a = d/c
1 + b/a = 1 + d/c
a/a + b/a = c/c + d/c
(a+b)/a = (c+d)/c
a/(a+b) = c/(c+d)
-------------------------------------------------------
Part (d)
The goal is to show that
(a+b)/(c+d) = b/d
leads to
a/b = c/d
so we can reverse it later.
(a+b)/(c+d) = b/d
d(a+b) = b(c+d)
ad+bd = bc+bd
ad = bc
a/b = c/d
Now reverse those steps
a/b = c/d
ad = bc
ad+bd = bc+bd
d(a+b) = b(c+d)
(a+b)/(c+d) = b/d
Let me know if you have any questions.
I recommend trying out numeric examples that the tutor @Theo has mentioned, or coming up with your own numbers to try out.
Keep in mind that the numeric examples do not constitute a full formal proof (since you'd need to check infinitely many numeric values).
The proof is when we did all those algebraic steps.
|
|
|