Question 1172719: I need help please, here is the problem:
The costs $C of making a school bag is partly constant and partly varies inversely as the total number N of bags made. When 200 bags are made, the cost per bag is $60. When 500 bags are made, the cost per bag is
$45. How many bags are made if the cost per bag is $40? Find the cost per bag if 400 bags are made.
Found 3 solutions by Solver92311, Theo, ikleyn:
Answer by Solver92311(821)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i could be wrong, but i believe this involves a straight line equation.
the general form of the straight line equation is y = mx + b.
m is the slope.
b is the y-intercept.
first find the slope.
you have two points.
they are (200,60) and (500,45)
the points are in (x,y) format.
x is the number of bags made and y is the cost per bag.
m is equal to the change in y divided by the change in x.
m = (45 - 60) / (500 - 200) = -15/300 = -1/20 = -.05
the general equation becomes y = -.05 * x + b
to solve for b, replace x and y with the value from either point.
i chose (200,60)
y = -.05 * x + b becomes 60 = -.05 * 200 + b
solve for b to get b = 60 + 10 = 70
the equation becomes y = -.05 * x + 70
using this equation, .....
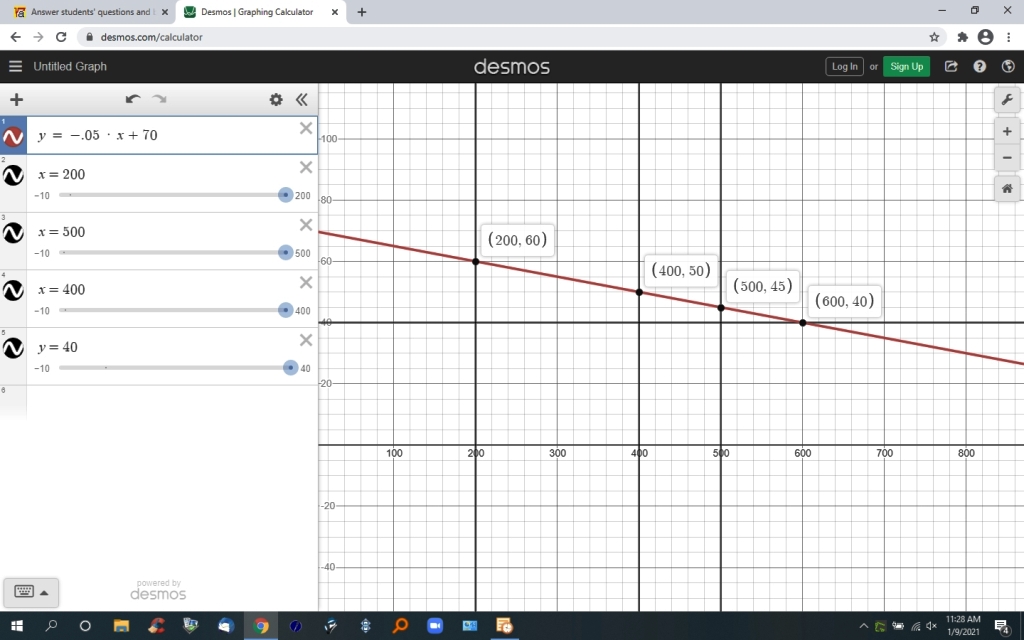
when x = 200, y = -.05 * 200 + 70 = 60
when x = 500, y = -.05 * 500 + 70 = 45
when x = 400, y = -.05 * 400 + 70 = 50
when y = 40, the equation becomes 40 = -.05 * x + 70
subtract 70 from both sides of the equation to get -30 = -.05 * x
solve for x to get x = -30 / -.05 = 600
the graph of that equation is shown below.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The costs $C of making a school bag is partly constant and partly varies inversely as the total number N of bags made.
When 200 bags are made, the cost per bag is $60. When 500 bags are made, the cost per bag is $45.
How many bags are made if the cost per bag is $40? Find the cost per bag if 400 bags are made.
~~~~~~~~~~~~~~~~~
The problem's formulation is TERRIBLE (!)
This language was in use at parish country schools of the before-Shakespearean times
and was totally changed and replaced starting from post-Newtonian era.
Now nobody understands this language --- the proofs are the posts of the two other English-speaking tutors.
The meaning of this post (if translate it to the contemporary English) is THIS :
Consider the function C(N) = A + (B/N), where "A" and "B" are constants, whose values are not known now.
Given : C(200) = 60 dollars, C(500) = 45 dollars.
Find N, if C(N) = 40 dollars.
OK, now I will start based on my re-formulation.
At N = 200, we have this equation
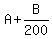 = 60 dollars (1)
At N = 500, we have this equation = 60 dollars (1)
At N = 500, we have this equation
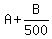 = 45 dollars (2)
Subtracting equation (2) from equation (1), you get = 45 dollars (2)
Subtracting equation (2) from equation (1), you get
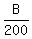 - - 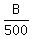 = 60-45 = 15
Multiply both sides by 1000. You will get
5B - 2B = 15000,
3B = 15000
B = 15000/3 = 5000.
Then from (2) = 60-45 = 15
Multiply both sides by 1000. You will get
5B - 2B = 15000,
3B = 15000
B = 15000/3 = 5000.
Then from (2)
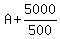 = 45, or
A + 10 = 45
A = 45 - 10 = 35.
To complete the solution, you need find N from the equation
C(N) = 40, or = 45, or
A + 10 = 45
A = 45 - 10 = 35.
To complete the solution, you need find N from the equation
C(N) = 40, or  = 40.
The last equation gives = 40.
The last equation gives
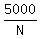 = 40-35 = 5
N = = 40-35 = 5
N =  = 1000.
ANSWER. N = 1000. = 1000.
ANSWER. N = 1000.
Solved, answered, explained and completed.
|
|
|