Question 1172711: A quantity y partly varies directly as x and partly varies inversely as x when x = 4, y = 17.
When x = 6, y = 13 , find the value of y when x = 10.
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A quantity y partly varies directly as x and partly varies inversely as x when x = 4, y = 17.
When x = 6, y = 13 , find the value of y when x = 10.
~~~~~~~~~~~~~
This formulation is terrible.
This problem uses forms of the language that go, probably, from Middle Ages.
It costed me huge efforts to guess what does it mean.
I do not think that an average modern/contemporary student can understand this language and the meaning.
Nevertheless . . .
The problem means that y is this function y = ax + 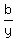 with unknown coefficient "a" and "b".
To find these coefficients, we have these equations from the condition
x= 4 : 4a + with unknown coefficient "a" and "b".
To find these coefficients, we have these equations from the condition
x= 4 : 4a + 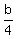 = 17 (1)
x = 6 : 6a + = 17 (1)
x = 6 : 6a +  = 13 (2)
To solve this system, multiply equation (1) by 4 (both sides); multiply equation (2) by 6 (both sides).
You will get
16a + b = 68 (3)
36a + b = 78 (4)
Subtract equation (3) from equation (4) to eliminate "b" and to get "a" :
36a - 16a = 78 - 68
20a = 10
a = 10/20 = 0.5.
Then from (3),
16*0.5 + b = 68,
b = 68 - 8 = 60.
Thus the function y is y = 0.5x + = 13 (2)
To solve this system, multiply equation (1) by 4 (both sides); multiply equation (2) by 6 (both sides).
You will get
16a + b = 68 (3)
36a + b = 78 (4)
Subtract equation (3) from equation (4) to eliminate "b" and to get "a" :
36a - 16a = 78 - 68
20a = 10
a = 10/20 = 0.5.
Then from (3),
16*0.5 + b = 68,
b = 68 - 8 = 60.
Thus the function y is y = 0.5x +  .
Hence, at x= 10, y = 0.5*10 + .
Hence, at x= 10, y = 0.5*10 + 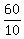 = 5 + 6 = 11. ANSWER = 5 + 6 = 11. ANSWER
Solved.
|
|
|