Question 1168642: If for three distinct positive numbers x, y, and z,

then find the numerical value of x/y.
Answer by ikleyn(52782)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If for three distinct positive numbers x, y, and z,
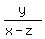 = = 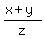 = = 
then find the numerical value of x/y.
~~~~~~~~~~~~~~
You are given two equations
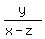 = =  (1) (1)
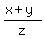 = =  (2)
In equation (1), divide the numerator and denominator of the left side by "y".
You can safely do it, because "y" is assumed to be positive.
In equation (2), divide the numerator and denominator of the left side by "y".
You can safely do it, due to the same reason.
Both left side sides in equations (1) and (2) will not change their values, so you will get an EQUIVALENT equations (2)
In equation (1), divide the numerator and denominator of the left side by "y".
You can safely do it, because "y" is assumed to be positive.
In equation (2), divide the numerator and denominator of the left side by "y".
You can safely do it, due to the same reason.
Both left side sides in equations (1) and (2) will not change their values, so you will get an EQUIVALENT equations
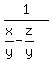 = =  (1') (1')
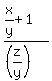 = =  (2')
Introduce new variables u = (2')
Introduce new variables u =  and v = and v = 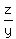 .
Our goal is to find the numerical value of "u".
You can write equation (1') and (2') in the form .
Our goal is to find the numerical value of "u".
You can write equation (1') and (2') in the form
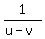 = u (3) = u (3)
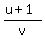 = u (4)
From equation (3), you have
u*(u-v) = 1. (5)
From equation (4) express v = = u (4)
From equation (3), you have
u*(u-v) = 1. (5)
From equation (4) express v = 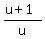 and substitute it into equation (5), replacing "v" there. You will get and substitute it into equation (5), replacing "v" there. You will get
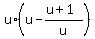 = 1, or = 1, or
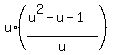 = 1, or = 1, or
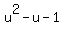 = 1, or = 1, or
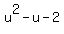 = 0. (6)
Equation (6) is a quadratic equation. Solve it by factoring
(u-2)*(u+1) = 0.
Thus it has two roots u= 2 and u= -1.
According to the condition, only positive value u= 2 is the solution to the problem.
So, the ANSWER to the problem's question is = 0. (6)
Equation (6) is a quadratic equation. Solve it by factoring
(u-2)*(u+1) = 0.
Thus it has two roots u= 2 and u= -1.
According to the condition, only positive value u= 2 is the solution to the problem.
So, the ANSWER to the problem's question is  = u = 2. = u = 2.
Solved.
|
|
|