SOLUTION: Tap A takes 6 minutes to fill a tank and Tap B takes 9 minutes to fill the same tank.Pipe C can empty the tank in 15 minutes.How long will it take to fill up the tank if the pipe i

Algebra ->  Proportions  -> Lessons -> SOLUTION: Tap A takes 6 minutes to fill a tank and Tap B takes 9 minutes to fill the same tank.Pipe C can empty the tank in 15 minutes.How long will it take to fill up the tank if the pipe i      Log On


   

Question 1147308: Tap A takes 6 minutes to fill a tank and Tap B takes 9 minutes to fill the same tank.Pipe C can empty the tank in 15 minutes.How long will it take to fill up the tank if the pipe is in use when both tapes are turned on?
Found 4 solutions by josgarithmetic, ikleyn, MathTherapy, greenestamps:
Answer by josgarithmetic(39616) About Me  (Show Source):
You can put this solution on YOUR website!
%281%2F6%2B1%2F9%29-1%2F15, fill rate if both taps and the pipe are open

%281%2F6%29%283%2F3%29%2B%281%2F9%29%282%2F2%29-1%2F15
%283%2B2%29%2F18-1%2F15
5%2F18-1%2F15
25%2F90-6%2F90
19%2F90
TIME-------90%2F19=4%2614%2F19minutes
4 minutes 44 seconds





cross%28%283-2%29%2F18-1%2F15%29
cross%281%2F18-1%2F15%29--------this will be a negative value. The tank will never become filled this way.

Answer by ikleyn(52776) About Me  (Show Source):
You can put this solution on YOUR website!
.
Tap A fills  1%2F6  of the tank volume per minute.


Tap B fills  1%2F9  of the tank volume per minute.


Pipe C drains  1%2F15  of the tank volume per minute.


When both taps and the tube work together, their combined rate of work is


    1%2F6 + 1%2F9 - 1%2F15 = 15%2F90 + 10%2F90 - 6%2F90 = %2815%2B10-6%29%2F90 = 19%2F90. 


of the tank volume per minute.


It means that the tank will be filled in  90%2F19 minutes = 4.737 minutes (approximately) = 4 minutes and 44 seconds (approximately).    ANSWER

Solved.

--------------------

It is a standard and typical joint work problem.

There is a wide variety of similar solved joint-work problems with detailed explanations in this site.  See the lessons
    - Using Fractions to solve word problems on joint work
    - Solving more complicated word problems on joint work
    - Selected joint-work word problems from the archive


Read them and get be trained in solving joint-work problems.

Also,  you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this textbook under the topic
"Rate of work and joint work problems"  of the section  "Word problems".


Save the link to this online textbook together with its description

Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson

to your archive and use it when it is needed.


Answer by MathTherapy(10551) About Me  (Show Source):
You can put this solution on YOUR website!
Tap A takes 6 minutes to fill a tank and Tap B takes 9 minutes to fill the same tank.Pipe C can empty the tank in 15 minutes.How long will it take to fill up the tank if the pipe is in use when both tapes are turned on?
FYI: This will NOT be a negative value! 

So, this is INCORRECT ======> 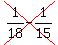cross%281%2F18-1%2F15%29 --------this will be a negative value.   The tank will never become filled this way..

It's filling FASTER than it's EMPTYING!

Correct answer: highlight_green%28matrix%281%2C4%2C+90%2F19%2C+or%2C+4%2614%2F19%2C+minutes%29%29

Answer by greenestamps(13198) About Me  (Show Source):
You can put this solution on YOUR website!


Once again, tutor @josgarithmetic sets up the problem correctly for solving and then botches the arithmetic to come up with a nonsensical answer. Clearly, if either tap alone can fill the tank faster than drain pipe can drain it, then with the two taps working together the tank will get filled at some point.

And once again, tutor @maththerapy states that the first solution is clearly wrong and then shows the answer without saying or showing anything about how to get the answer, making the response useless to the student.

And tutor @ikleyn, as usual, presents a clear and correct solution to the problem, using the standard algebraic approach.

Here is an alternative to that approach that many students prefer because it avoids working with fractions.

Consider the least common multiple of the three given times. The LCM of 6, 9, and 15 is 90.

Now suppose we have 90 minutes, and there are multiple tanks to be filled.

Tap A can fill 90/6 = 15 tanks in 90 minutes; tap B can fill 90/9 = 10 tanks in 90 minutes. And the drain pipe C can empty 90/15 = 6 tanks in 90 minutes.

So in 90 minutes the number of tanks that could be filled is 15+10-6 = 19.

And since in 90 minutes 19 tanks could be filled, the one tank can be filled in 90/19 minutes.