SOLUTION: A tap can fill a tank in 6 mins and another can fill the same tank in 8 mins .How long will it take to fill the tank if the two taps were opened at the same time?

Click here to see ALL problems on Proportions

Question 1099571: A tap can fill a tank in 6 mins and another can fill the same tank in 8 mins .How long will it take to fill the tank if the two taps were opened at the same time?
Found 3 solutions by Theo, Fombitz, Edwin McCravy:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website!
rate * time = quantity

first tap fills the tank in 6 minutes.
rate for the first tap is 1/6 of the tank in 1 minute.

second tap fills the tank in 8 minutes.
rate for the second tap is 1/8 of the tank in 1 minute.

when they are both open, their rates are additive.

1/6 + 1/8 = 4/24 + 3/24 = 7/24

their combined rate is 7/24 of the tap in 1 minute when they are both open.

rate * time = quantity.

rate is 7/24 of the tank in 1 minute.
time is what you want to find
quantity is 1 full tank

formula becomes 7/24 * time = 1

solve for time to get time = 1 * 24/7 = 24/7 minutes = 3 and 3/7 minutes.

Answer by Fombitz(32388)   (Show Source):
You can put this solution on YOUR website!
Rate x Time = Output
.
.
.

.
.

.
.
So when they're working together,

Answer by Edwin McCravy(20056)   (Show Source):
You can put this solution on YOUR website!
A tap can fill a tank in 6 mins

So the 1st tap's filling rate is 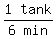or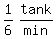

and another can fill the same tank in 8 mins .

So the 2nd tap's filling rate is or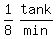

How long will it take to fill the tank if the two taps were opened at the same time?

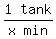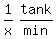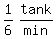
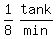
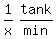
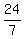
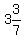
Let the answer be x mins. So together they can fill 1 tank in x minutes So their combined filling rate is or Their combined filling rate must be equal to the sum of their filling rates: Multiply through by the LCD of 24x Edwin