SOLUTION: If a:b =c:d =5:7, find (a+c):(b+d).

Algebra ->  Proportions  -> Lessons -> SOLUTION: If a:b =c:d =5:7, find (a+c):(b+d).      Log On


   

Question 1013841: If a:b =c:d =5:7, find (a+c):(b+d).
Found 2 solutions by MathLover1, Theo:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

If a%3Ab+=c%3Ad+=5%3A7, find %28a%2Bc%29%3A%28b%2Bd%29
a%3Ab+=5%3A7
7a=5b
a=5b%2F7

c%3Ad+=5%3A7
7c=5d
c=5d%2F7

=>
%28a%2Bc%29%3A%28b%2Bd%29
=%285b%2F7%2B5d%2F7%29%3A%28b%2Bd%29
=%28%285b%2B5d%29%2F7%29%3A%28b%2Bd%29
=%285%28b%2Bd%29%29%2F7%29%3A%28b%2Bd%29
=%285%28b%2Bd%29%29%2F7%29%2F%28b%2Bd%29
=5%28b%2Bd%29%2F7%28b%2Bd%29
=5%2F7


Answer by Theo(13342) About Me  (Show Source):
You can put this solution on YOUR website!
your solution is (a+c)/(b+d) = 5/7.

you can find it easily by just assuming some values for a and b and c and d and solving.

you can also find it in terms of a and b and c and d much more arduously by performing algebra on the variables directly.

in that case you will get (a+c)/(b+d) = (25*(b+d))/(49*(a+c)).

when you replace a and b and c and d with qualifying numbers, the ratio will wind up being the same, i.e. it will be 5/7.

first i'll do it using numbers.

then i'll do it using variables.

your ratio is a:b = c:d = 5:7.

this can also be written as a/b = c/d = 5/7

this means that a/b = 5/7 and that c/d = 5/7.

if we assume that a is 5 and b is 7, then the ratio is 5/7 for them.

if we assume that c is 5 and d is 7, then the ratio is 5/7 for them.

since a = 5 and b = 7 and c = 5 and d = 7, then the ratio of (a+c)/(b+d) becomes (5+5)/(7+7) which becomes 10/14 which simplifies to 5/7.

you can assume that c = 10 and d = 14, or c = 15 and d = 21.
as long as the ratio of c/d simplifies to 5/7, all those values are good and will lead to the same conclusion.

for example:

assume a = 5 and b = 7 and c = 15 and d = 21.

(a+c) = 20
(b + d) = 28

(a+c)/(b+d) = 20/28 which simplifies to 5/7.

with letters it becomes a little more complex, but you'll get an answer that will be equivalent to the answer that you got with numbers.

start with a/b = 5/7 and c/d = 5/7

cross multiply to get 7a = 5b and 7c = 5d

solve for a to get a = 5b/7
solve for b to get b = 7a/5
solve for c to get c = 5d/7
solve for d to get d = 7c/5

a+c is equal to 5b/7 + 5d/7 = (5b+5d)/7 = 5(b+d)/7.

b+d is equal to 7a/5 + 7c/5 = (7a+7c)/5 = 7(a+c)/5.

(a+c)/(b+d) = 5(b+d)/7 divided by 7(a+c)/5.

this is equivalent to 5(b+d)/7 times 5/(7(a+c))

this is equivalent to 5(b+d)*5/ (7*7(a+c))

simplify further to get 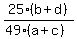25%28b%2Bd%29%2F%2849%28a%2Bc%29%29

to confirm, we replace a,b,c,d with qualifying values.

we'll assume a = 5, b = 7, c = 15, d = 21

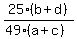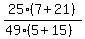
the equation of 25%28b%2Bd%29%2F%2849%28a%2Bc%29%29 becomes 25%287%2B21%29%2F%2849%285%2B15%29%29

simplify this to get %2825%2A28%29%2F%2849%2A20%29

perform the multiplication to get 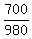700%2F980

when you simplify this, you will find that it is equal to 5/7.