Tutors Answer Your Questions about Proportions (FREE)
Question 1172902: In a class of 50 students 24 like football 21 basketball and cricket six like football and basketball 3 like basketball only, five like all three games, and 14 did not like any of the three games.
1.illustrate this information of Venn diagram
2. Find the number of students who like
A. Football and cricket
B. Exactly one of the game
C. Exactly two of the game.
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In a class of 50 students, 24 like football, 21 basketball and cricket, six like football and basketball,
3 like basketball only, five like all three games, and 14 did not like any of the three games.
1.illustrate this information of Venn diagram
2. Find the number of students who like
A. Football and cricket
B. Exactly one of the game
C. Exactly two of the game.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution to this problem in the post by @CPhill is INCORRECT.
The error is that @CPhill incorrectly reads/interprets the problem.
Indeed, when retelling what are given, he writes n(B) = 21, and then uses it in his solution.
It is INCORRECT. n(B) = 21 is NOT given.
What is given in the problem is n(B∩ C) = 21.
Therefore, everything what follows in the post by @CPhill is irrelevant and incorrect.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Regarding the post by @CPhill . . .
Keep in mind that @CPhill is a pseudonym for the Google artificial intelligence.
The artificial intelligence is like a baby now. It is in the experimental stage
of development and can make mistakes and produce nonsense without any embarrassment.
It has no feeling of shame - it is shameless.
This time, again, it made an error.
Although the @CPhill' solutions are copy-paste Google AI solutions, there is one essential difference.
Every time, Google AI makes a note at the end of its solutions that Google AI is experimental
and can make errors/mistakes.
All @CPhill' solutions are copy-paste of Google AI solutions, with one difference:
@PChill never makes this notice and never says that his solutions are copy-past that of Google.
So, he NEVER SAYS TRUTH.
Every time, @CPhill embarrassed to tell the truth.
But I am not embarrassing to tell the truth, as it is my duty at this forum.
And the last my comment.
When you obtain such posts from @CPhill, remember, that NOBODY is responsible for their correctness,
until the specialists and experts will check and confirm their correctness.
Without it, their reliability is ZERO and their creadability is ZERO, too.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Absolutely, let's solve this problem step-by-step using a Venn diagram.
**1. Venn Diagram**
Let's use the following notation:
* F = Football
* B = Basketball
* C = Cricket
We are given:
* Total students = 50
* n(F) = 24
* n(B) = 21
* n(F ∩ B) = 6
* Students who like basketball DISABLED_event_only= 3
* n(F ∩ B ∩ C) = 5
* Students who like none of the games = 14
Here's how we'll build the Venn diagram:
1. **Start with the intersection of all three:**
* n(F ∩ B ∩ C) = 5. Place 5 in the center of the Venn diagram where all three circles overlap.
2. **Football and Basketball:**
* n(F ∩ B) = 6. We know 5 like all three, so 6 - 5 = 1 student likes only football and basketball. Place 1 in the F ∩ B region.
3. **Basketball Only:**
* 3 students like only basketball, place a 3 in the B only section of the venn diagram.
4. **Basketball circle:**
* We know n(B)=21. We have 5+1+3=9 of those students accounted for. 21-9=12. We do not yet know how many of those 12 like cricket, so we will fill in the values that we can.
5. **Students who like none:**
* 14 students like none of the games. Place 14 outside the circles.
6. **Total within the circles:**
* 50 total students - 14 who like none = 36 students who like at least one sport.
7. **Football circle:**
* n(F) = 24. We know 5+1=6 of those. 24-6=18. 18 students like football and cricket, or football only. We cannot yet determine the individual values.
8. **Cricket values:**
* We can find the total amount of students that like cricket. 36 students total like at least one sport. 36 - 3 - 1 - 5 - 18 = 9. 9 students like cricket only or cricket and football. We cannot yet determine the individual values.
9. **Completing the diagram:**
* We know that the remaining students that like basketball must total 12. Let x= the students that like basketball and cricket only. 12 = x+5. x=7. 7 students like Basketball and Cricket only.
* We know the students that like cricket total 9+7+5 = 21.
* We know that the football only students equal 24-1-5-students that like football and cricket only. 24-6-cricket and football DISABLED_event_only= football only. 21-5-7=9. 9 students like cricket only. 24-1-5 = 18. 21-9-5-7=0. 18-0=18. 18 students like football only.
* The Venn diagram is complete.
**2. Answers**
**A. Football and Cricket:**
* To find the number of students who like football and cricket, we add the students who like only football and cricket (0) and those who like all three (5): 0+5=5.
* 5 students like football and cricket.
**B. Exactly One Game:**
* Add the number of students who like only football (18), only basketball (3), and only cricket (9): 18 + 3 + 9 = 30.
* 30 students like exactly one game.
**C. Exactly Two Games:**
* Add the number of students who like football and basketball only (1), basketball and cricket only (7), and football and cricket only (0): 1 + 7 + 0 = 8.
* 8 students like exactly two games.
Question 1209747: A ladder leans against a vertical wall if the height of the wall is 12m calculate the length of the ladder
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! I can't calculate the length of the ladder with only the height of the wall. I need more information, such as:
* **The angle the ladder makes with the ground or the wall:** This angle is crucial for determining the ladder's length.
* **The distance from the base of the ladder to the wall:** This distance, along with the wall's height, forms a right triangle, allowing us to use the Pythagorean theorem.
**Here's why I need more information:**
Imagine the ladder leaning against the wall. You can make the ladder very short (almost vertical) or very long (almost horizontal) while still reaching the 12m height. The height alone doesn't fix the length.
**Example:**
If you tell me the ladder is 13 meters from the base of the wall, I can use the Pythagorean theorem:
* a² + b² = c² (where a and b are the sides of the right triangle, and c is the hypotenuse - the ladder)
* 12² + 13² = c²
* 144 + 169 = c²
* 313 = c²
* c = √313
* c ≈ 17.69 meters
So, in this *example*, the ladder would be approximately 17.69 meters long. But I need the correct information from you to do the calculation for your specific problem.
Question 1209606: A ship traveling a straight course sights a lighthouse at an angle of A=21.3 deg as shown in Fig. 340. After traveling another B=2.26 mi, the lighthouse is at an angle of C=45.9 deg. Determine x and y. Not sure how i should submit the picture however.
Found 2 solutions by timofer, math_tutor2020:
Answer by timofer(104)  (Show Source): (Show Source):
You can put this solution on YOUR website! The description if that with nothing else must plainly specify the meaning of x and of y.
We can only guess that y is for how tall the lighthouse, and x to be one of the horizontal distances.
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
There isn't a way for students to upload images directly to algebra.com
You should upload the picture to an image hosting website, and then share the link.
Question 1209464: If x-3 is directly proportional to the square of y and x =5 when y=2,
What is x when y=6
Found 2 solutions by greenestamps, josgarithmetic:
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The response from the other tutor shows a formal solution using the definition of direct variation to find the constant of proportionality and solves the problem from there.
That is a good approach, and it would probably be the best approach if we needed to find the solutions for several different sets of data.
But when the problem only requires us to find the answer for a single new set of data, we can use the definition of direct variation to solve the problem informally and quickly.
In this problem, we are given that (x-3) is directly proportional to the square of y; and we are asked to find the value of x when y is 6, given that x is 5 when y is 2.
So the y value increases by a factor of 3 (from 2 to 6); since (x-3) is directly proportional to the square of y, the value of (x-3) increases by a factor of 3^2 = 9.
Originally, the value of x-3 was 5-3 = 2; 2 increased by a factor of 9 is 2*9 = 18.
So the new value of x-3 is 18, which means the new value of x is 18+3 = 21.
ANSWER: 21
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1209463: If x-3 is directly proportional to the square of y and x= 5 when y = 2 when x when y= 6
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
D U P L I C A T E
Just solved at this forum today under this link
https://www.algebra.com/algebra/homework/proportions/Proportions.faq.question.1209464.html
Question 1209085: Three runners, Dirk, Edith, and Foley all start at the same time for a 24 km race, and each of them runs at a constant speed. When Dirk finishes the race, Edith is 10 km behind, and Foley is 8 km behind. When Edith finishes the race, how far behind is Foley, in km?
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Three runners, Dirk, Edith, and Foley all start at the same time for a 24 km race,
and each of them runs at a constant speed.
When Dirk finishes the race, Edith is 10 km behind, and Foley is 8 km behind  . .
When Edith finishes the race, how far behind is Foley, in km?
~~~~~~~~~~~~~~~~~~~~
From the problem, when Dirk completed the race, Edith ran 24-10 = 14 kilometers;
Foley ran 14- 8 = 6 kilometers.
From it, we conclude that Edith rate to Foley rate ratio is 14/6.
So, when Edith will complete 24 kilometers, the ratio of distances Edith and Foley run
will be the same 14/6. It gives the proportion
24 14
---------- = ----.
Foley ran 6
From this proportion
Foley run (when Edith finished) =  = = 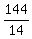 = =  = 10.28571 kilometers.
Hence, when Edith finishes the rate, Foley is 24-10.2857 = 13.7143 kilometers behind (rounded value). = 10.28571 kilometers.
Hence, when Edith finishes the rate, Foley is 24-10.2857 = 13.7143 kilometers behind (rounded value).
Solved.
Question 1209086: Five workers have been hired to complete a job. If one additional worker is hired, they could complete the job 6 days earlier. If the job needs to be completed 32 days earlier, how many additional workers should be hired?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 40 extra workers
Explanation
Let's say the job is to move 9000 boxes.
I'm picking this value since it's a multiple of 5 and 6.
You can change 9000 to anything else you want to get the same answer at the end.
If there are 5 workers, then each worker handles 9000/5 = 1800 boxes.
Each worker has a unit rate of 1800/x boxes per day.
x is the number of days to finish the job with 5 workers.
rate = amountDone/time
When there are 6 workers, each person now gets 9000/6 = 1500 boxes.
The unit rate per person is 1500/(x-6) where the x-6 refers to finishing the job 6 days early compared to the previous scenario.
If we assume each worker has the same unit rate, then we get this equation
1800/x = 1500/(x-6)
Solving it leads to x = 36.
I'll let the student handle the scratch work.
It takes 36 days for 5 workers to do the job.
It takes 30 days for 6 workers to do the same job.
Each worker moves 50 boxes per day because 1800/36 = 50 or 1500/30 = 50.
n = number of additional workers to hire
n+5 = total number of workers when including the original 5 workers
9000/(n+5) = number of boxes each worker handles
The goal is to finish 32 days early. So instead of taking 36 days it should take 36-32 = 4 days
rate*time = amount done
(50 boxes per day)*(4 days) = 9000/(n+5) boxes
50*4 = 9000/(n+5)
Solving for n leads to n = 40
I'll let the student handle the scratch work.
More practice with a similar question is found here
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Five workers have been hired to complete a job.
If one additional worker is hired, they could complete the job 6 days earlier.
If the job needs to be completed 32 days earlier, how many additional workers should be hired?
~~~~~~~~~~~~~~~
Solve it step by step.
Step 1 - determine the number of days needed for 5 workers
to complete the job.
Let d be the number of days for 5 workers to complete the job.
Then the entire job is 5d worker-days.
6 workers could complete the job in (d-6) days.
Hence, from this perspective, the entire work is 6*(d-6) worker-days.
It gives us this equation
5d = 6(d-6),
from which we get
5d = 6d - 36 ---> 36 = 6d - 5d ---> 36 = d.
Hence, 5 workers need 36 days to complete the job, and the entire job is 5*36 = 180 worker-days.
Step 2 - determine the number of workers needed
to complete the job in 32 days earlier.
The question wants the job be complete in 36-32 = 4 days.
It requires 180/4 = 45 workers.
Step 3 - determine the number of additional workers
to be hired.
The number of additional workers is 45 - 5 = 40.
ANSWER. 40 additional workers should be hired to complete the job in 32 days earlier.
Solved.
Question 1208723: Ruth has a beaker containing a solution of $800$ mL of acid and $200$ mL of water. She thinks the solution is a little strong, so she drains $300$ mL from the beaker, adds $300$ mL of water, and stirs the solution. Ruth thinks the solution is still too strong, so again she drains $400$ mL from the beaker, and adds $400$ mL of water. Ruth again thinks the solution is still too strong, so again she drains $100$ mL from the beaker, and adds $100$ mL of water. How many mL of water are now in the beaker?
Found 4 solutions by mccravyedwin, ikleyn, MathTherapy, Edwin McCravy:
Answer by mccravyedwin(406)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Ikleyn says:
The answer by Edwin is incorrect.
I can't find any mistake. I've gone through it several times and cannot find it.
Edwin
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Ruth has a beaker containing a solution of 800 mL of acid and 200 mL of water.
She thinks the solution is a little strong, so she drains 300 mL from the beaker, adds 300 mL of water, and stirs the solution.
Ruth thinks the solution is still too strong, so again she drains 400 mL from the beaker, and adds 400 mL of water.
Ruth again thinks the solution is still too strong, so again she drains 100 mL from the beaker, and adds 100 mL of water.
How many mL of water are now in the beaker?
~~~~~~~~~~~~~~~~~~~~~~
The answers in the posts by Edwin and by @MathThearapy are different - so, there is the need to check their solutions.
Here I make this check, but I use slightly different methodology, which better suits to the problem.
In this problem, after each step, Ruth keeps the total volume of the mixture in the beaker unchangeable, 1000 mL.
Therefore, in my solution, I calculate and watch/track for the concentration/amount of the acid, only, in the beaker.
I will calculate the amount of water in the beaker after the last step, but will not calculate/watch/track it at the intermediate steps.
It will allow me to reduce the volume of calculations and will allow me to concentrate
my attention on one component, only (which is acid). It will diminish the volume
of calculations and will diminish possible errors.
(0) Starting amount of the acid is 800 mL; the starting concentration is  = 0.8.
(1) First step is to drain 300 mL of the mixture from the beaker.
With it, 0.8*300 = 240 mL of the acid goes out.
The amount of the acid remained in the beaker is 800-240 = 560 mL.
The amount of water is added to keep the total volume of the mixture in the beaker 1000 mL.
The concentration after step 1 is = 0.8.
(1) First step is to drain 300 mL of the mixture from the beaker.
With it, 0.8*300 = 240 mL of the acid goes out.
The amount of the acid remained in the beaker is 800-240 = 560 mL.
The amount of water is added to keep the total volume of the mixture in the beaker 1000 mL.
The concentration after step 1 is 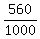 = 0.56.
(2) Second step is to drain 400 mL of the mixture from the beaker.
With it, 0.56*400 = 224 mL of the acid goes out.
The amount of the acid remained in the beaker is 560-224 = 336 mL.
The amount of water is added to keep the total volume of the mixture in the beaker 1000 mL.
The concentration after step 2 is = 0.56.
(2) Second step is to drain 400 mL of the mixture from the beaker.
With it, 0.56*400 = 224 mL of the acid goes out.
The amount of the acid remained in the beaker is 560-224 = 336 mL.
The amount of water is added to keep the total volume of the mixture in the beaker 1000 mL.
The concentration after step 2 is  = 0.336.
(3) Third step is to drain 100 mL of the mixture from the beaker.
With it, 0.336*100 = 33.6 mL of the acid goes out.
The amount of the acid remained in the beaker is 336-33.6 = 302.4 mL.
The amount of water is added to keep the total volume of the mixture in the beaker 1000 mL.
Hence, the amount of water in the beaker is 1000 - 302.4 = 697.6 mL.
ANSWER. The amount of water in the beaker after step 3 is 697.6 mL. = 0.336.
(3) Third step is to drain 100 mL of the mixture from the beaker.
With it, 0.336*100 = 33.6 mL of the acid goes out.
The amount of the acid remained in the beaker is 336-33.6 = 302.4 mL.
The amount of water is added to keep the total volume of the mixture in the beaker 1000 mL.
Hence, the amount of water in the beaker is 1000 - 302.4 = 697.6 mL.
ANSWER. The amount of water in the beaker after step 3 is 697.6 mL.
Solved.
The answer by @MathTherapy is confirmed.
Calculations are made by the most economic/effective way.
Of course, the most important element of my post
is the METHODOLOGY, which EXCLUDES unnecessary calculations.
The answer by Edwin is incorrect.
//////////////////////////////
To help Edwin to identify his error, I copied and pasted here his solution
from his post, and pointed the precise place/line with the error.
Ruth has a beaker containing a solution of 800 mL of acid and 200 mL of water.
She thinks the solution is a little strong, so she drains 300 mL from the
beaker, adds 300 mL of water, and stirs the solution. Ruth thinks the solution
is still too strong, so again she drains 400 mL from the beaker, and adds 400 mL
of water. Ruth again thinks the solution is still too strong, so again she
drains 100 mL from the beaker, and adds 100 mL of water. How many mL of water
are now in the beaker?
I'll keep track of the liquid, acid, water, % acid, and % water, because in
other problems like this you might be asked different amounts and percentages.
Ruth has a beaker containing a solution of 800 mL of acid and 200 mL of water.
liquid = 800+200 = 1000 mL
acid = 800 mL
water = 200 mL
% acid = 800/1000 = 0.8 = 80%
% water = 200/1000 = 0.2 = 20%
She thinks the solution is a little strong, so she drains 300 mL from the beaker,
liquid = 1000-300 = 700 mL
acid = (0.8)(700) = 560 mL
water = (0.2)(700) = 140 mL
% acid = 80%
% water = 20%
adds 300 mL of water, and stirs the solution.
liquid = 700+300 = 1000 mL
acid = 560 mL
water = 140+300 = 440 mL
% acid = 560/1000 = 0.56 = 56%
% water = 440/1000 = 0.44 = 44%
Ruth thinks the solution is still too strong, so again she drains 400 mL from the beaker,
liquid = 1000-400 = 600 mL
acid = (600)(0.56) = 336 mL
water = (600)(0.44) = 264 mL
% acid = 56%
% water = 44%
and adds 400 mL of water.
liquid = 600+400=1000 mL
acid = 336 mL
water = 264+400=664 mL
% acid = 336/1000=33.6%
% water = 664/1000=66.4%
Ruth again thinks the solution is still too strong, so again she drains 100 mL from the beaker,
liquid = 1000-100=900 mL
acid = (900)(0.336) = 302.4 mL <<<---=== The error is HERE. The correct calculation should be acid = 1000*0.336 = 336 mL,
with relevant correction in all consequential calcs.
water = 664-100=564 mL
% acid = 33.6%
% water = 66.4%
and adds 100 mL of water.
liquid = 900+100=1000 mL
acid = 302.4 mL
water = 564+100=664 mL
% acid = 302.4/1000 0.3024=30.24%
% water = 664/1000 = 0.664 = 66.4%
How many mL of water are now in the beaker?
664 mL <-- ANSWER
Edwin
...................................
This shows once again how dangerous is to split your attention
by making unnecessary calculations.
Professional writers in such cases say: how good that this mistake was made naturally;
otherwise, it would have been worth to make it intentionally, and then talking, discussing
and teaching on how to organize calculations in a secure way.
@ikleyn
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Ruth has a beaker containing a solution of $800$ mL of acid and $200$ mL of water. She thinks the solution is a little strong, so she drains $300$ mL from the beaker, adds $300$ mL of water, and stirs the solution. Ruth thinks the solution is still too strong, so again she drains $400$ mL from the beaker, and adds $400$ mL of water. Ruth again thinks the solution is still too strong, so again she drains $100$ mL from the beaker, and adds $100$ mL of water. How many mL of water are now in the beaker?
 .
From the above TABLE:
Start: Amount of acid: 800 mL ; amount of water: 200 mL ; Total in solution: 800 + 200 = 1,000 mL ; % acid: .
From the above TABLE:
Start: Amount of acid: 800 mL ; amount of water: 200 mL ; Total in solution: 800 + 200 = 1,000 mL ; % acid:  % water:
% water:  1. DRAINING 300 mL of solution: 1,000 - 300 = 700 mL of solution left, of which 560 mL is acid and 140 mL is water
2. ADDING 300 mL of water: Solution = 700 + 300 = 1,000 mL, of which 560 mL is STILL acid and 140 + 300 = 440 mL, is water.
Acid in solution:
1. DRAINING 300 mL of solution: 1,000 - 300 = 700 mL of solution left, of which 560 mL is acid and 140 mL is water
2. ADDING 300 mL of water: Solution = 700 + 300 = 1,000 mL, of which 560 mL is STILL acid and 140 + 300 = 440 mL, is water.
Acid in solution:  ; Water in solution: ; Water in solution:  3. DRAINING 400 mL of solution: 1,000 - 400 = 600 mL of solution left, of which 56%, or 336 mL is acid and 264 mL is water
4. ADDING 400 mL of water: Solution = 600 + 400 = 1,000 mL, of which 336 mL is STILL acid and 264 + 400 = 664 mL, is water.
Acid in solution:
3. DRAINING 400 mL of solution: 1,000 - 400 = 600 mL of solution left, of which 56%, or 336 mL is acid and 264 mL is water
4. ADDING 400 mL of water: Solution = 600 + 400 = 1,000 mL, of which 336 mL is STILL acid and 264 + 400 = 664 mL, is water.
Acid in solution:  ; Water in solution: ; Water in solution:  5. DRAINING 100 mL of solution: 1,000 - 100 = 900 mL of solution left, of which 33.6%, or 302.4 mL is acid, and 900 - 302.4, or 597.6 mL is water
6. Finally, ADDING 100 mL of water: Solution = 900 + 100 = 1,000 mL, of which 302.4 mL is STILL acid and 1,000 - 302.4 = 697.6 mL, is water.
I hope you're able to follow this!
Sir Edwin,
Where @Ikleyn says the error is, is NOT where it is. I'll copy part of yours to show you the errors.
Ruth again thinks the solution is still too strong, so again she drains 100 mL from the beaker,
liquid = 1000-100=900 mL
acid = (900)(0.336) = 302.4 mL <==== The error is NOT HERE, as per @Ikleyn. This is FINE!
water = 664-100=564 mL <==== The error is HERE. 100 mL was DRAINED, so 100 mL should NOT HAVE been
subtracted from water. In fact, the REMAINING 900 mL, after 100 mL was drained
includes 302.4 mL (33.6%) acid, and 597.6 (900 - 302.4) mL, or 66.4% water.
% acid = 33.6%
% water = 66.4%
and adds 100 mL of water.
liquid = 900+100=1000 mL
acid = 302.4 mL
water = 564+100=664 mL <==== Instead of 564 mL HERE, the STARTING amount of water should be 597.6 mL; and,
with 100 mL ADDED, water becomes 597.6 + 100 = 697.6 mL!
% acid = 302.4/1000 0.3024=30.24%
% water = 664/1000 = 0.664 = 66.4% <==== Instead of 664/1,000, this should be 697.6/1,000 = 69.76%, which makes
FINAL acid and water percentages, 30.24 and 69.76, for a TOTAL of 100%.
How many mL of water are now in the beaker?
664 mL <-- ANSWER
697.6 mL <-- ANSWER <==== Should be.
Edwin
5. DRAINING 100 mL of solution: 1,000 - 100 = 900 mL of solution left, of which 33.6%, or 302.4 mL is acid, and 900 - 302.4, or 597.6 mL is water
6. Finally, ADDING 100 mL of water: Solution = 900 + 100 = 1,000 mL, of which 302.4 mL is STILL acid and 1,000 - 302.4 = 697.6 mL, is water.
I hope you're able to follow this!
Sir Edwin,
Where @Ikleyn says the error is, is NOT where it is. I'll copy part of yours to show you the errors.
Ruth again thinks the solution is still too strong, so again she drains 100 mL from the beaker,
liquid = 1000-100=900 mL
acid = (900)(0.336) = 302.4 mL <==== The error is NOT HERE, as per @Ikleyn. This is FINE!
water = 664-100=564 mL <==== The error is HERE. 100 mL was DRAINED, so 100 mL should NOT HAVE been
subtracted from water. In fact, the REMAINING 900 mL, after 100 mL was drained
includes 302.4 mL (33.6%) acid, and 597.6 (900 - 302.4) mL, or 66.4% water.
% acid = 33.6%
% water = 66.4%
and adds 100 mL of water.
liquid = 900+100=1000 mL
acid = 302.4 mL
water = 564+100=664 mL <==== Instead of 564 mL HERE, the STARTING amount of water should be 597.6 mL; and,
with 100 mL ADDED, water becomes 597.6 + 100 = 697.6 mL!
% acid = 302.4/1000 0.3024=30.24%
% water = 664/1000 = 0.664 = 66.4% <==== Instead of 664/1,000, this should be 697.6/1,000 = 69.76%, which makes
FINAL acid and water percentages, 30.24 and 69.76, for a TOTAL of 100%.
How many mL of water are now in the beaker?
664 mL <-- ANSWER
697.6 mL <-- ANSWER <==== Should be.
Edwin
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
First, I'll copy and paste your problem here so I can delete those "$" dollar
marks around every number. They confuse me. We didn't do that where I came
from. J
Ruth has a beaker containing a solution of 800 mL of acid and 200 mL of water.
She thinks the solution is a little strong, so she drains 300 mL from the
beaker, adds 300 mL of water, and stirs the solution. Ruth thinks the solution
is still too strong, so again she drains 400 mL from the beaker, and adds 400 mL
of water. Ruth again thinks the solution is still too strong, so again she
drains 100 mL from the beaker, and adds 100 mL of water. How many mL of water
are now in the beaker?
I'll keep track of the liquid, acid, water, % acid, and % water, because in
other problems like this you might be asked different amounts and percentages.
Ruth has a beaker containing a solution of 800 mL of acid and 200 mL of water.
liquid = 800+200 = 1000 mL
acid = 800 mL
water = 200 mL
% acid = 800/1000 = 0.8 = 80%
% water = 200/1000 = 0.2 = 20%
She thinks the solution is a little strong, so she drains 300 mL from the beaker,
liquid = 1000-300 = 700 mL
acid = (0.8)(700) = 560 mL
water = (0.2)(700) = 140 mL
% acid = 80%
% water = 20%
adds 300 mL of water, and stirs the solution.
liquid = 700+300 = 1000 mL
acid = 560 mL
water = 140+300 = 440 mL
% acid = 560/1000 = 0.56 = 56%
% water = 440/1000 = 0.44 = 44%
Ruth thinks the solution is still too strong, so again she drains 400 mL from the beaker,
liquid = 1000-400 = 600 mL
acid = (600)(0.56) = 336 mL
water = (600)(0.44) = 264 mL
% acid = 56%
% water = 44%
and adds 400 mL of water.
liquid = 600+400=1000 mL
acid = 336 mL
water = 264+400=664 mL
% acid = 336/1000=33.6%
% water = 664/1000=66.4%
Ruth again thinks the solution is still too strong, so again she drains 100 mL from the beaker,
liquid = 1000-100=900 mL
acid = (900)(0.336) = 302.4 mL
water = 664-100=564 mL
% acid = 33.6%
% water = 66.4%
and adds 100 mL of water.
liquid = 900+100=1000 mL
acid = 302.4 mL
water = 564+100=664 mL
% acid = 302.4/1000 0.3024=30.24%
% water = 664/1000 = 0.664 = 66.4%
How many mL of water are now in the beaker?
664 mL <-- ANSWER
Edwin
Question 1208771: The weight of 66 eggs is shown. Identify the constant of proportionality of total weight to number of eggs.
The weight of 6 eggs is 258 g.
Found 5 solutions by Alan3354, timofer, greenestamps, josgarithmetic, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by timofer(104)  (Show Source): (Show Source):
You can put this solution on YOUR website! What do you want here exactly? Unit conversion? Where is shown this weight of the 66 eggs?
If 6 eggs are 258 grams, then you have this.
 so this is 43 grams per egg. so this is 43 grams per egg.
If you have 66 eggs then their weight is  grams grams
or better 2.84 kilograms.
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The underlying concept here -- not at all clearly stated -- is that the total weight is directly proportional to the number of eggs.
E = # of eggs
W = weight
k = constant of proportionality
W = k*E
Using the given information that the weight of 6 eggs is 258g,
258 = k*6
k = 258/6 = 43
ANSWER: The constant of proportionality is 43 (grams per egg)
Note we could equally well say that the number of eggs is directly proportional to the total weight -- in which case the constant of proportionality would be (1/43) eggs per gram.
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The weight of 66 eggs is shown. Identify the constant of proportionality of total weight to number of eggs.
The weight of 6 eggs is 258 g.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
As I read this post, I see two inconsistent statements/messages there
without any visible logical connection between them.
Look, think, check, re-check, double-check, cross-check, fix, and write
your request in a proper human language, clearly saying what is given
and what you want to get (to learn). Do not use excessive words (if you know what it means).
Then re-post.
Question 1208740: Five workers have been hired to complete a job. If one additional worker is hired, they could complete the job 10 days earlier. If the job needs to be completed 32 days earlier, how many additional workers should be hired?
Found 4 solutions by ikleyn, josgarithmetic, math_tutor2020, Edwin McCravy:
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Five workers have been hired to complete a job. If one additional worker is hired,
they could complete the job 10 days earlier. If the job needs to be completed 32 days earlier,
how many additional workers should be hired?
~~~~~~~~~~~~~~~~~~~~~
I am 999% sure that the problem in the post is printed incorrectly and has a typo.
My interior voice tells me, and I am 99% sure that the correct formulation is THIS
Five workers have been hired to complete a job. If one additional worker is hired,
they could complete the job 10 days earlier. If the job needs to be completed  days earlier,
how many additional workers should be hired? days earlier,
how many additional workers should be hired?
I will solve the problem in this edited formulation.
SOLUTION
Let "a" be the rate of work of one worker per day.
Then the number of days for 5 workers to complete the job is  ;
the number of days for 6 workers to complete the job is ;
the number of days for 6 workers to complete the job is  .
Thus, we can write this time equation .
Thus, we can write this time equation
 - -  = 10 days. (1)
It implies = 10 days. (1)
It implies
 - -  = 10, = 10,
 = 10,
a = = 10,
a =  . (2)
+----------------------------------------------------------------+
| Thus, we found that under given condition the rate of work |
| is 1/300 of the job per day for each worker. |
+----------------------------------------------------------------+
Now we want to find the number n of additional workers (to 5 workers) to complete
the job 32 days earlier. For it, we write similar time equation to (1) . (2)
+----------------------------------------------------------------+
| Thus, we found that under given condition the rate of work |
| is 1/300 of the job per day for each worker. |
+----------------------------------------------------------------+
Now we want to find the number n of additional workers (to 5 workers) to complete
the job 32 days earlier. For it, we write similar time equation to (1)
 - -  = 30.
Substitute here a = 1/300, based on (2). You will get = 30.
Substitute here a = 1/300, based on (2). You will get
 - -  = 30.
To solve, simplify step by step. You will get
60 - = 30.
To solve, simplify step by step. You will get
60 - 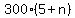 = 30,
60 - 30 = = 30,
60 - 30 =  ,
30 = ,
30 =  5 + n =
5 + n =  5 + n = 10.
n = 10 - 5 = 5.
+----------------------------------------------------------------+
| Second part of the solution can be worded in different way. |
+----------------------------------------------------------------+
We just found that the rate of work of one worker is 1/300 of the job per day.
It means that the entire job is 300 man-days.
5 workers can complete this job in 300/5 = 60 days.
We want the job be complete in 60-30 = 30 days.
For it, 300/30 = 10 workers are needed, hence, 10 - 5 = 5 workers should be added.
ANSWER. 5 workers should be hired in addition to the original 5 workers to complete the job 32 days earlier.
5 + n = 10.
n = 10 - 5 = 5.
+----------------------------------------------------------------+
| Second part of the solution can be worded in different way. |
+----------------------------------------------------------------+
We just found that the rate of work of one worker is 1/300 of the job per day.
It means that the entire job is 300 man-days.
5 workers can complete this job in 300/5 = 60 days.
We want the job be complete in 60-30 = 30 days.
For it, 300/30 = 10 workers are needed, hence, 10 - 5 = 5 workers should be added.
ANSWER. 5 workers should be hired in addition to the original 5 workers to complete the job 32 days earlier.
Solved.
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
You can put this solution on YOUR website! r, work rate of 1 worker
x, number of days work
1, number of jobs
n, how many additional workers, for the question

First two equations allows to solve for x.
and then,...
.
.
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
I have edited your question to remove the dollar signs.
It seems to be a strange copy/paste error.
My method isn't as efficient compared with tutor Edwin's method, but it's another viewpoint to think about at least.
Let's say the job is moving 9000 boxes.
The number 9000 can be changed to any positive whole number and the final answer will be the same.
I'm picking this value since it's a multiple of 5 and 6.
We have these two key assumptions:
1. Each worker moves boxes at the same rate.
2. None of the workers slow down any others.
If there are 9000 boxes, and 5 workers on the job, then each person handles 9000/5 = 1800 boxes.
x = number of days to finish the job if there are 5 workers
rate*time = amount done
rate = (amount done)/time
rate = 1800/x
If there are 5 workers, each handling 1800 boxes, then each person moves 1800/x boxes per day.
This is the unit rate per worker.
..............................................
Now introduce another worker to have 5+1 = 6 workers.
Each worker now handles 9000/6 = 1500 boxes.
This extra worker brings the original number of days x to x-10 since this expanded group can complete the job 10 days earlier.
We find the unit rate per worker is 1500/(x-10) boxes per day.
Using assumption #1 mentioned earlier, we can solve 1800/x = 1500/(x-10) to get x = 60 which is the number of days it takes if you had 5 workers.
We determine that the unit rate per worker is 1800/x = 1800/60 = 30 boxes per day (or you could compute it like this 1500/(x-10) = 1500/(60-10) = 30)
Also we determine it takes x-10 = 60-10 = 50 days if you had 6 workers.
..............................................
We want the job to finish 32 days early, so we want the duration to be x-32 = 60-32 = 28 days instead of the initial 60.
n = number of extra workers you need to hire
n+5 = number of workers you'll have total when considering the initial 5
9000/(n+5) = number of boxes each worker handles
rate*time = amount done
(30 boxes per day)*(28 days) = 9000/(n+5)
30*28 = 9000/(n+5)
840 = 9000/(n+5)
840*(n+5) = 9000
840n+4200 = 9000
840n = 9000 - 4200
840n = 4800
n = 4800/840
n = 5.7142857 approximately
Note that the mixed number 5 & 5/7 is equal to 5.7142857 approximately, so this matches what Edwin got.
Obviously it's not possible to hire 0.714 of a worker, so we need to round up to n = 6. It's likely some of the workers won't have much to do as the job is getting closer to the end.
--------------------------------------------------------------------------
Answer: 6 additional workers
A similar question found here and also here
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
Question 1208722: A plane flies from Penthaven to Jackson and then back to Penthaven. When there is no wind, the round trip takes $5$ hours and $20$ minutes, but when there is a wind blowing from Penthaven to Jackson at $70$ miles per hour, the trip takes $9$ hours. How many miles is the distance from Penthaven to Jackson?
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A plane flies from Penthaven to Jackson and then back to Penthaven. When there is no wind, the round trip takes 5 hours and 20 minutes,
but when there is a wind blowing from Penthaven to Jackson at 70 miles per hour, the trip takes 9 hours.
How many miles is the distance from Penthaven to Jackson?
~~~~~~~~~~~~~~~~~~~
Let "d" be the distance from Penthaven to Jackson, in miles.
Let "u" be the speed of the plane in still air (at no wind), in miles per hour.
Since the round trip is 5 hours and 20 minutes, we can write an equation
 = 5 = 5 hours,
or
2d = hours,
or
2d =  , d = , d = 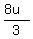 .
Next, the speed of the plane with the wind is u+70 mph and the travel time with the wind is .
Next, the speed of the plane with the wind is u+70 mph and the travel time with the wind is
 = = 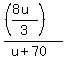 = = 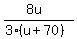 .
Next, the speed of the plane against the wind is u-70 mph and the travel time against the wind is .
Next, the speed of the plane against the wind is u-70 mph and the travel time against the wind is
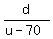 = =  = = 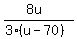 .
So, the time equation for the round trip with and against the wind is .
So, the time equation for the round trip with and against the wind is
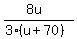 + + 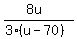 = 9.
+----------------------------------------------------------------------+
| At this point, the setup is complete. Now our task is |
| to solve this equation and to find the own speed "u" of the plane. |
+----------------------------------------------------------------------+
For it, multiply both sides of this equation by 3*(u+70*(u-70). You will get
8u(u+70) + 8u(u-70) = 9*3*(u+70)*(u-70),
8u^2 + 560u + 8u^2 - 560u = 27*(u^2 - 4900),
8u^2 + 8u^2 = 27u^2 - 27*4900,
27*4900 = 27u^2 - 8u^2 - 8u^2
27*4900 = 11u^2
u = = 9.
+----------------------------------------------------------------------+
| At this point, the setup is complete. Now our task is |
| to solve this equation and to find the own speed "u" of the plane. |
+----------------------------------------------------------------------+
For it, multiply both sides of this equation by 3*(u+70*(u-70). You will get
8u(u+70) + 8u(u-70) = 9*3*(u+70)*(u-70),
8u^2 + 560u + 8u^2 - 560u = 27*(u^2 - 4900),
8u^2 + 8u^2 = 27u^2 - 27*4900,
27*4900 = 27u^2 - 8u^2 - 8u^2
27*4900 = 11u^2
u =  = 109.669 miles per hour.
Thus the own speed of the plane at no wind is 109.669 miles per hour.
Hence, the distance from Penthaven to Jackson is d = = 109.669 miles per hour.
Thus the own speed of the plane at no wind is 109.669 miles per hour.
Hence, the distance from Penthaven to Jackson is d = 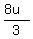 = =  = 292.451 miles.
ANSWER. The distance from Penthaven to Jackson is about 292.5 miles. = 292.451 miles.
ANSWER. The distance from Penthaven to Jackson is about 292.5 miles.
Solved.
The method, which I showed in this post, is a normal, regular and standard method solving similar problems.
On the way, I fixed the error which tutor/professor Edwin made in his post.
I do not think that a/the school teacher would accept the solution presented by Edwin.
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website! A plane flies from Penthaven to Jackson and then back to Penthaven. When there is no wind, the round trip takes $5$ hours and $20$ minutes, but when there is a wind blowing from Penthaven to Jackson at $70$ miles per hour, the trip takes $9$ hours. How many miles is the distance from Penthaven to Jackson?
Let the ground speed of the plane when there is no wind = R mph
When the wind is a tail wind of 70 mph, the ground speed is R+70 mph
When the wind is a head wind of 70 mph, the ground speed is R-70 mph
Let T1 = the time to go from P to J against a head wind.
Let T2 = the time to go from J to P with a tail wind.
|distance| rate | time |
P to J to P (no wind) | 2D | R | 5 2/3 |
P to J (head wind) | D | R-70 | T1 |
J to P (tail wind) | D | R+70 | T2 |
 Find a solver online for nonlinear systems. Perhaps
https://www.wolframalpha.com/
Use t for T1 and T for T2
since they don't usually take subscripted letters.
D≈325.89, R≈115.02, t≈1.7614, T≈7.2386
So the distance is approximately 326 miles.
Edwin
Find a solver online for nonlinear systems. Perhaps
https://www.wolframalpha.com/
Use t for T1 and T for T2
since they don't usually take subscripted letters.
D≈325.89, R≈115.02, t≈1.7614, T≈7.2386
So the distance is approximately 326 miles.
Edwin
Question 1208277: What is the unit rate of 524 cars over 4 weeks? I'm confused.
Found 2 solutions by ikleyn, josgarithmetic:
Answer by ikleyn(52778)   (Show Source): (Show Source):
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
You can put this solution on YOUR website! Unit might be for ONE week. Exactly which choice depends on what exactly you were given and asked for.
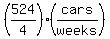
 ----------------- 131 cars in any single week ----------------- 131 cars in any single week
Question 1208049: the scale of a detailed map is 1:2000. find the actual area, in square meters for 1 cm squared
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
One centimeter in the map is 2000 centimeters in the field, or 20 meters.
The square 1 cm by 1 cm in the map is the square of 20 meters by 20 meters in the field,
or 20*20 = 400 m^2 actual area.
Question 1207797: A tank is filled with 360 liters of water. A hole at the bottom of the tank allows the water to drain at a constant rate of 0.2 liters per second. How many minutes will it take to completely empty the tank?
Found 4 solutions by ikleyn, math_tutor2020, josgarithmetic, MathLover1:
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
My approach to such problems is " solve as simple as it is possible ".
If there is a simplest way, it is preferable.
This problem can be solved arithmetically, without using fractions and without using equations.
It is a good exercise to develop skills on counting and to develop common sense.
A constant rate 0.2 liter per second means 1 (one) liter in 5 seconds.
So, the time to empty this tank is 360*5 = 1800 seconds.
To get minutes, divide 1800 seconds by 60 seconds, because 1 minute is 60 seconds.
ANSWER. 1800/60 = 180/6 = 30 minutes.
Solved.
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 30 minutes
Explanation
x = number of seconds that elapse
The tank starts off completely full at 360 liters.
The drain rate is a constant 0.2 liters per second.
After x seconds elapse, the tank loses 0.2x liters of water.
There are 360-0.2x liters remaining.
The tank is empty when 0 liters remain.
We'll set the previous expression equal to 0 to solve for x.
360-0.2x = 0
360 = 0.2x
x = 360/0.2
x = 1800
It takes 1800 seconds for the tank to completely empty.
Divide by 60 to convert from seconds to minutes.
1800 seconds = 1800/60 = 30 minutes is the final answer.
Side note:
I'm not too familiar with physics so I could be wrong, but I have a feeling that the water won't drain at a constant rate in reality.
I have a feeling it's more of a case of "more water --> faster drain rate" since gravity is pulling on more mass and hence more of a downward force is applied.
Regardless of this, it's probably best to stick to the assumption of a constant rate since the textbook stated as such. We're in a theoretical framework anyway.
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1207765: Mitch made two 10-inch pizzas using a recipe that calls for 3 cups
of flour and 3/4 cup of water. Mitch wants to make more pizzas
without changing the ratio of flour to water.
Complete the sentence about the ingredients Mitch needs to make
eight 10-inch pizzas. Enter a number that makes the sentence
true.
To make eight 10-inch pizzas, Mitch uses 12 cups of flour and
__?__ cups of water.
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 3 cups of water
Explanation
To make 2 pizzas, he needs 3 cups of flour.
To make 8 pizzas, he needs 12 cups of flour.
This is a jump of "times 4".
Quadrupling the original amount of water has us go from 3/4 cups to (3/4)*4 = 3 cups
Another way to find this answer is to solve this proportion
3/0.75 = 12/x
Question 1207033: Patricia is making cookies and has a gallon of milk for a recipe. Each batch of 36 cookies takes 1 cup of milk. What is the maximum number of cookies Patricia can make? (Assume that only a full batch of cookies can be made. No partial batches!)
1 gallon = 128 ounces
1 cup = 8 ounces
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Patricia is making cookies and has a gallon of milk for a recipe.
Each batch of 36 cookies takes 1 cup of milk.
What is the maximum number of cookies Patricia can make?
(Assume that only a full batch of cookies can be made. No partial batches!)
1 gallon = 128 ounces
1 cup = 8 ounces
~~~~~~~~~~~~~~~~~~~~~~~~
The number of cups in one gallon is equal to 128/8 = 16.
The number of batches is equal to the number of cups, i.e. 16.
The number of cookies is the product 16*36 = 576. ANSWER
Solved.
Question 614764: A car begins a trip with 12 gallons of gasoline in the tank and ended with 7 1/2 gallons. The car traveled 17.3 miles for each gallon of gasoline. During the trip gasoline was bought for $10.00, at a cost of $1.25 per gallon. The total number of miles traveled during the trip was most nearly
A)79
B)196
C)216
D)229
E)236
Found 2 solutions by ikleyn, josgarithmetic:
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Total volume of gasoline spent is 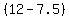 + + 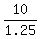 = 4.5 + 8 = 12.5 gallons.
Total distance traveled is 12.5*17.3 = 216.25 miles.
ANSWER. Option C). = 4.5 + 8 = 12.5 gallons.
Total distance traveled is 12.5*17.3 = 216.25 miles.
ANSWER. Option C).
Solved.
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1206961: Find the missing terms
x:y:7=6:8:20
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The last number in the first set is 7/20 of the last number in the third set; so each number in the first set is 7/20 of the corresponding number in the second set.
x = 6*(7/20)
y = 8*(7/20)
Perform the multiplications and express the results in whatever form is required.
Question 1099257: Three no are in continued proportion .if mean proportional is 12 and sum of other two is 26 then find the no
Found 2 solutions by greenestamps, mananth:
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A formal mathematical solution as provided by the other tutor is fine; the student should understand how to solve the problem by that method.
However, if a formal mathematical solution is not required, the problem is easily solved mentally if the student understands the given information.
The given information tells us that we are looking for two numbers whose sum is 26 and whose product is 12^2=144.
144 = 12*12; sum is 12+12=24
144 = 16*9; sum is 16+9=25
144 = 18*8; sum is 18+8=26
ANSWER: the numbers are 8, 12, and 18
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! Three no are in continued proportion .if mean proportional is 12 and sum of other two is 26 then find the numbers
a/b = b/c
b=12
a/12=12/c
ac = 144
a =144/c
a+c =26
substitute a
144/c +c =26
multiply equation by c
144 +c^2 = 26c
c^2-26c+144=0
c^2-26c=-144
Add 169 to both sides
c^2-26c +169 =169- 144
(c-13)^2= 25
take the square rooton both sides
(c-13)=+ /- 5
either c-13 = 5 or c-13 = -5
c= 18 or c= 8
ac =144
a = 144/18 or 144/8
a= 8 or 18
Question 1206294: a bag contains 6 red marbles 9 blue marbles and 5green marbles. you randomly select one marble from the bag what is the probability that the marble is red?
Found 2 solutions by ikleyn, kilofighters:
Answer by ikleyn(52778)   (Show Source): (Show Source):
Answer by kilofighters(2)   (Show Source): (Show Source):
Question 1206066: As a nurse, part of your daily duties is to mix medications in the proper proportions for your patients. For one of your regular patients, you always mix Medication A with Medication B in the same proportion. Last week, your patient's doctor indicated that you should mix 100 milligrams of Medication A with 150 milligrams of Medication B. However this week, the doctor said to only use 75 milligrams of Medication B. How many milligrams of Medication A should be mixed this week?
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
This week, you are instructed to use only 75 mg of medication B,
which is half of the previous dosage of 150 mg of medication B.
So, to keep the same proportion, you should use one half
of the previous dosage medication A, which half is 50 mg of A. ANSWER
Hope it is clear.
Question 1206013: beatriz built a model of a tower using 600 bricks stacked vertically that are each 0.25 inch tall. The actual tower is 200 feet tall. What is the scale of her model?
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
beatriz built a model of a tower using 600 bricks stacked vertically that are each 0.25 inch tall.
The actual tower is 200 feet tall. What is the scale of her model?
~~~~~~~~~~~~~~~~~~~~~
The model is 600 * 0.25 inch = 150 inches tall.
The tower is 200 feet tall, or 200 * 12 = 2400 inches.
The scale is this ratio 150 : 2400 = 1 : 16.
In other words, 1 inch of the model corresponds to 16 inches of real construction.
Question 1205953: Consider the following data.
Group 1 Group 2 Group 3
Men 38 48 71
Women 6 49 30
Create the conditional data distribution in each of the groups given that the person was male. (Round your answers to the nearest integer.)
Group 1 Group 2 Group 3 Total
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer:
| Group 1 | Group 2 | Group 3 | Total | | Men | 24% | 31% | 45% | 100% |
Explanation:
There are 38+48+71 = 157 men surveyed.
Divide each male group count by 157 to find the corresponding percentages
38/157 = 0.242 = 24.2%
48/157 = 0.306 = 30.6%
71/157 = 0.452 = 45.2%
Each result is approximate.
Then round each result to the nearest integer
24.2% --> 24%
30.6% --> 31%
45.2% --> 45%
As a check, the percentages should add to 100%
24+31+45 = 100
This helps confirm the answers.
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265
|




