Question 1208722: A plane flies from Penthaven to Jackson and then back to Penthaven. When there is no wind, the round trip takes $5$ hours and $20$ minutes, but when there is a wind blowing from Penthaven to Jackson at $70$ miles per hour, the trip takes $9$ hours. How many miles is the distance from Penthaven to Jackson?
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20077)   (Show Source): (Show Source):
You can put this solution on YOUR website! A plane flies from Penthaven to Jackson and then back to Penthaven. When there is no wind, the round trip takes $5$ hours and $20$ minutes, but when there is a wind blowing from Penthaven to Jackson at $70$ miles per hour, the trip takes $9$ hours. How many miles is the distance from Penthaven to Jackson?
Let the ground speed of the plane when there is no wind = R mph
When the wind is a tail wind of 70 mph, the ground speed is R+70 mph
When the wind is a head wind of 70 mph, the ground speed is R-70 mph
Let T1 = the time to go from P to J against a head wind.
Let T2 = the time to go from J to P with a tail wind.
|distance| rate | time |
P to J to P (no wind) | 2D | R | 5 2/3 |
P to J (head wind) | D | R-70 | T1 |
J to P (tail wind) | D | R+70 | T2 |
 Find a solver online for nonlinear systems. Perhaps
https://www.wolframalpha.com/
Use t for T1 and T for T2
since they don't usually take subscripted letters.
D≈325.89, R≈115.02, t≈1.7614, T≈7.2386
So the distance is approximately 326 miles.
Edwin
Find a solver online for nonlinear systems. Perhaps
https://www.wolframalpha.com/
Use t for T1 and T for T2
since they don't usually take subscripted letters.
D≈325.89, R≈115.02, t≈1.7614, T≈7.2386
So the distance is approximately 326 miles.
Edwin
Answer by ikleyn(53431)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A plane flies from Penthaven to Jackson and then back to Penthaven. When there is no wind, the round trip takes 5 hours and 20 minutes,
but when there is a wind blowing from Penthaven to Jackson at 70 miles per hour, the trip takes 9 hours.
How many miles is the distance from Penthaven to Jackson?
~~~~~~~~~~~~~~~~~~~
Let "d" be the distance from Penthaven to Jackson, in miles.
Let "u" be the speed of the plane in still air (at no wind), in miles per hour.
Since the round trip is 5 hours and 20 minutes, we can write an equation
 = 5 = 5 hours,
or
2d = hours,
or
2d =  , d = , d = 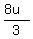 .
Next, the speed of the plane with the wind is u+70 mph and the travel time with the wind is .
Next, the speed of the plane with the wind is u+70 mph and the travel time with the wind is
 = = 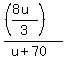 = = 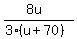 .
Next, the speed of the plane against the wind is u-70 mph and the travel time against the wind is .
Next, the speed of the plane against the wind is u-70 mph and the travel time against the wind is
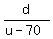 = =  = = 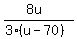 .
So, the time equation for the round trip with and against the wind is .
So, the time equation for the round trip with and against the wind is
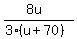 + + 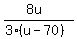 = 9.
+----------------------------------------------------------------------+
| At this point, the setup is complete. Now our task is |
| to solve this equation and to find the own speed "u" of the plane. |
+----------------------------------------------------------------------+
For it, multiply both sides of this equation by 3*(u+70*(u-70). You will get
8u(u+70) + 8u(u-70) = 9*3*(u+70)*(u-70),
8u^2 + 560u + 8u^2 - 560u = 27*(u^2 - 4900),
8u^2 + 8u^2 = 27u^2 - 27*4900,
27*4900 = 27u^2 - 8u^2 - 8u^2
27*4900 = 11u^2
u = = 9.
+----------------------------------------------------------------------+
| At this point, the setup is complete. Now our task is |
| to solve this equation and to find the own speed "u" of the plane. |
+----------------------------------------------------------------------+
For it, multiply both sides of this equation by 3*(u+70*(u-70). You will get
8u(u+70) + 8u(u-70) = 9*3*(u+70)*(u-70),
8u^2 + 560u + 8u^2 - 560u = 27*(u^2 - 4900),
8u^2 + 8u^2 = 27u^2 - 27*4900,
27*4900 = 27u^2 - 8u^2 - 8u^2
27*4900 = 11u^2
u =  = 109.669 miles per hour.
Thus the own speed of the plane at no wind is 109.669 miles per hour.
Hence, the distance from Penthaven to Jackson is d = = 109.669 miles per hour.
Thus the own speed of the plane at no wind is 109.669 miles per hour.
Hence, the distance from Penthaven to Jackson is d = 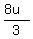 = =  = 292.451 miles.
ANSWER. The distance from Penthaven to Jackson is about 292.5 miles. = 292.451 miles.
ANSWER. The distance from Penthaven to Jackson is about 292.5 miles.
Solved.
The method, which I showed in this post, is a normal, regular and standard method solving similar problems.
On the way, I fixed the error which tutor/professor Edwin made in his post.
I do not think that a/the school teacher would accept the solution presented by Edwin.
|
|
|