Question 1132246: there are 1000 students in a college. there are also 1000 lockers which are all opened. all the 1000 students are required to perform the following exercise: the first student should go round to change the state of all the lockers ( that is if a locker is opened it should be closed, if a locker is closed, it should be opened. the second student should start with the second locker and change the state of all the lockers which are multiples of 2 ( that is 2,4,6 etc. up to the 1000th locker). the third student should start with third fourth locker changing the state of all lockers which are multiples of 3. that is all the lockers at 3,6,9,12.... positions till all the 1000 lockers are attended to. the forth student should start with the fourth locker changing the state of all lockers which are multiples of 4. that 4,8,12... till all the 1000 lockers are visited. the exercise should be done with all the students changing all the state of all lockers starting from their position and the multiples of lockers at their corresponding positions until the 1000th student change the state of the 1000th locker. at the end of the exercise, how many lockers remained closed? explain your strategy or strategies used to arrive at your solution
Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website! .
It is very well known problem, and you can find many solutions in the Internet or even at this forum's archive.
The difference is only in the form of presenting the solution.
Below I present my own version of the solution.
Let N be the number (the label) of some current locker. So, N is the number between 1 and 1000.
Let  ,  ,  , . . . ,  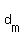be the divisors of the number N in the ascending order, from 1 to N inclusively.
The initial/original state of the locker N is "OPEN".
Notice that if the number of the current step is not a divisor of N, then the status of the locker N is not changed at this step.
It is changed if and only if the number of the step is the divisor of the number N.
Every time, when the number of the step is the divisor of N, the status of the locker is changed to the opposite one.
Thus, at the step it will be changed to the opposite status "CLOSED".
Further, at the step the status will be changed to the opposite status "OPEN".
At the step , the status will be changed to the opposite status "CLOSED".
And so on . . .
So, if the number N has EVEN number of divisors in the set , , , . . . , ,
then the locker N will have the same final status after completing the full procedure as its original status.
On the contrary, if the number N has ODD number of divisors in the set , , , . . . , ,
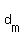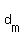then the locker N will have the opposite status after completing the full procedure comparing with its original status.
In other words, if the number N has EVEN number of divisors, its final status will be "OPEN".
Otherwise, if the number N has ODD number of divisors, its final status will be "CLOSED".
Now, if N = 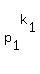 . .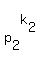 . .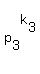 .  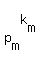is the decomposition
of the number N into the product of prime numbers, then the number of divisors is  . . . . .  .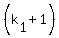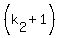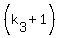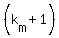
This number is ODD if and only if each factor of the last product is odd.
In other words, the number of divisors of the given number N is odd if and only if each prime in its prime decomposition has an EVEN degree.
It means that the number of divisors of the given number N is odd if and only if it is A SQUARE.
Returning to our problem, the numbers N of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, . . . , 1000 for which the final status
of the locker N will be "CLOSED" are the squares 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, . . . ,  = 961.
There are exactly 31 such numbers.
For the rest values N of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, . . . , 1000 the final status of the locker N will be "OPEN",
and the number of such lockers is 1000-31 = 969.
ANSWER. At the end of exercise, 31 lockers will be closed.
|
|
|
