Question 1012045: The 250 soldiers in a camp had enough food for forty days, After 10 days, 50 soldiers joined them. For how long will the remaining food last them? Solve using variation.
Found 2 solutions by ValorousDawn, MathTherapy:
Answer by ValorousDawn(53)   (Show Source): (Show Source):
You can put this solution on YOUR website! I don't even think variation is a legitimate way to solve this problem but here's something.
Lets say each soldier eats 1 food unit every day. Forty days for 250 soldiers is 10,000 food units. After 10 days, they are down to 10,000-250*10=8,750. If there are now  , they then subsequently will eat 300 food units a day. They will have food for , they then subsequently will eat 300 food units a day. They will have food for  days. If you must round, you'd round down, for 29 days. days. If you must round, you'd round down, for 29 days.
Answer by MathTherapy(10559)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The 250 soldiers in a camp had enough food for forty days, After 10 days, 50 soldiers joined them. For how long will the remaining food last them? Solve using variation.
Let S be number of soldiers, k = constant of variation, j = amount of food, and T = time



k = 250(40), or 10,000
Let fraction consumed after 10 days, be j




j, or fraction consumed after 10 days = 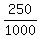 , or , or 
With  of food consumed of food consumed  remains, and 300 (250 + 50) soldiers are in camp remains, and 300 (250 + 50) soldiers are in camp



300T = 7,500 ------- Cross-multiplying
T, or time the remaining  of food will last = of food will last = 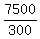 , or , or  days days
|
|
|