Question 899100: Prove by mathematical induction that 3^(2n)-8n-1, n is a positive integer, is a multiple of 64
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! Prove by mathematical induction that 3^(2n)-8n-1, n is a positive integer, is a multiple of 64
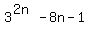 Let's rewrite
Let's rewrite 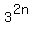 as as 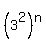 or or 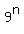 So we have to prove that
So we have to prove that
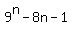 is a multiple of 64.
Prove true for n=1 is a multiple of 64.
Prove true for n=1
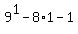 = = 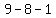 = =  0 is a multiple of every number so it's a multiple of 64.
But since that doesn't satisfy some people, we'll prove
it true for n=2 as well.
0 is a multiple of every number so it's a multiple of 64.
But since that doesn't satisfy some people, we'll prove
it true for n=2 as well.
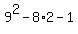 = = 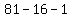 = =  So let k be any value, such as 1 or 2, that we've proved it for.
Then if that is the case then there is aome positive integer M,
such that
(1)
So let k be any value, such as 1 or 2, that we've proved it for.
Then if that is the case then there is aome positive integer M,
such that
(1) 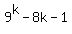 = = 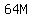 Now let's investigate to see what we must end up with if we are to
prove the proposition. Let's substitute k+1 for n and see what we are
going to have to end up with:
Now let's investigate to see what we must end up with if we are to
prove the proposition. Let's substitute k+1 for n and see what we are
going to have to end up with:
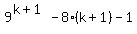
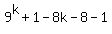
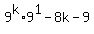 (2)
(2) 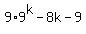 Now let's divide (1) into (2) by long division to see what we'll
have to multiply the left side of (1) by to get (2).
We start with this long division, which is a little weird because
we have something to the k power instead of k to some power, but
that's OK:
-----------------
9k-8k-1)9*9k - 8k - 9
9k goes into 9*9k 9 times, so we put 9 as a quotient and then
multiply and subtract to find the remainder of 64k
9
-----------------
9k-8k-1)9*9k - 8k - 9
9*9k - 72k - 9
----------------
64k
So the division gives
(3)
Now let's divide (1) into (2) by long division to see what we'll
have to multiply the left side of (1) by to get (2).
We start with this long division, which is a little weird because
we have something to the k power instead of k to some power, but
that's OK:
-----------------
9k-8k-1)9*9k - 8k - 9
9k goes into 9*9k 9 times, so we put 9 as a quotient and then
multiply and subtract to find the remainder of 64k
9
-----------------
9k-8k-1)9*9k - 8k - 9
9*9k - 72k - 9
----------------
64k
So the division gives
(3) 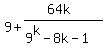 So that's what we have to multiply both sides of (1) by in order
to get the left side of (2). But notice that we are assuming that
we already have a value of 64M for which (1) is true, so we can
replace the denominator of (3) by 64M and get
(4)
So that's what we have to multiply both sides of (1) by in order
to get the left side of (2). But notice that we are assuming that
we already have a value of 64M for which (1) is true, so we can
replace the denominator of (3) by 64M and get
(4) 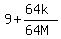 = = 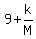 So we multiply the left side of (1) by (3) and the right side of (1)
by (4) since they are equal.
So we multiply the left side of (1) by (3) and the right side of (1)
by (4) since they are equal.
 = = 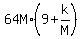 And we have already shown by the long division that the left side will
become the left side of (2), so we don't need to multiply it out, (but
you can if you like) and we will multiply out the right side
And we have already shown by the long division that the left side will
become the left side of (2), so we don't need to multiply it out, (but
you can if you like) and we will multiply out the right side
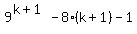 = = 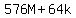 and we can show that the right side is a multiple of 64 because
and we can show that the right side is a multiple of 64 because
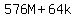 = =  So since we know that the proposition holds when n=k=1 and n=k=2, then
it must be true for n=k=3. Then if it is true for n=k=3 then it is true for
n=k=4, etc. etc. So it is true for all integer values of n.
Edwin
So since we know that the proposition holds when n=k=1 and n=k=2, then
it must be true for n=k=3. Then if it is true for n=k=3 then it is true for
n=k=4, etc. etc. So it is true for all integer values of n.
Edwin
|
|
|