SOLUTION: I need help please. A foot tall tree casts a shadow that is one foot shorter than the distance from the tip of the shadow to the top of the tree. Find the length of shadow. (a) L

Algebra ->  Test -> SOLUTION: I need help please. A foot tall tree casts a shadow that is one foot shorter than the distance from the tip of the shadow to the top of the tree. Find the length of shadow. (a) L      Log On


   

Question 874044: I need help please.
A foot tall tree casts a shadow that is one foot shorter than the distance from the tip of the shadow to the top of the tree. Find the length of shadow.
(a) Let x represent the length of the shadow. Write an expression for the diagonal distance from the tip of the shadow to the top of the tree.
(B) What is the length of the shadow? (Hint use the pythagorean formula)
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
Is it a 1-foot tall tree?
Is it an h-foot tall tree?
How tall is that tree?
If you do not have a number for the tree's height,
it gets a little more complicated.

If the height of the tree (in feet) is h ,
x is the length of the shadow in feet, then
x%2B1 is the diagonal distance from the tip of the shadow to the top of the tree, in feet,
and it is like this (drawing not to scale, lengths in feet):
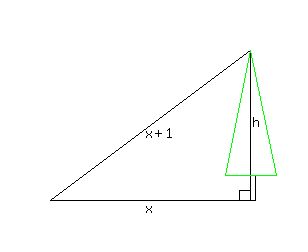%28x%2B1%29%5E2=x%5E2%2Bh%5E2<--->x%2B1=sqrt%28x%5E2%2Bh%5E2%29

If you do not know the height of the tree, all you can get is formulas to calculate those distances.
In that case,
a) x%2B1=sqrt%28x%5E2%2Bh%5E2%29 is the diagonal distance from the tip of the shadow to the top of the tree, in feet,
b) %28x%2B1%29%5E2=x%5E2%2Bh%5E2<--->x%5E2%2B2x%2B1=x%5E2%2Bh%5E2<--->2x%2B1=h%5E2<--->2x=h%5E2-1<--->x=%28h%5E2-1%29%2F2 is the length of the shadow.

If you knew the height of the tree,
you could substitute the value sooner rather than later,
and the algebra would get easier.
For example for a 3-foot tall tree, h=3 ,
%28x%2B1%29%5E2=x%5E2%2B3%5E2<--->%28x%2B1%29%5E2=x%5E2%2B9<--->x%2B1=sqrt%28x%5E2%2B9%29 ,
and to solve for x we write
%28x%2B1%29%5E2=x%5E2%2B9<--->x%5E2%2B2x%2B1=x%5E2%2B9<--->2x%2B1=9<--->2x=9-1<--->2x=8<--->x=8%2F2<--->x=4 .

For a 5-foot tall tree, h=5 ,
%28x%2B1%29%5E2=x%5E2%2B5%5E2<--->%28x%2B1%29%5E2=x%5E2%2B25<--->highlight%28x%2B1=sqrt%28x%5E2%2B25%29%29 is "an expression for the diagonal distance from the tip of the shadow to the top of the tree."
B) To solve for x (the length of the shadow in feet) we write
%28x%2B1%29%5E2=x%5E2%2B25<--->x%5E2%2B2x%2B1=x%5E2%2B25<--->2x%2B1=25<--->2x=25-1<--->2x=24<--->x=24%2F2<--->highlight%28x=12%29 .
The length of the shadow is 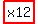highlight%28x12%29 feet.