SOLUTION: Find the number of distinguishable permutations of the letters int he words Alabama,algebra and florida

If "ALABAMA" were written so that the A's were of different colors,
like this, "ALABAMA", the number of permutations would be 7!.  However,
since the four A's look exactly alike in "ALABAMA", the number of
distinguishable permutations is much smaller.  So what we do is start 
with the 7! arrangements of "ALABAMA", and divide by the number of ways
the four A's can be arranged within each permutation, so that in effect
they will all be counted only once.

So the answer is 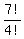 =  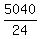= 210. 

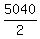"ALGEBRA" has  =  = 2520 distinguishable permutations, we only need 
to divide by 2 because there are only 2 A's that are indistinguishable.

FLORIDA has 7! = 5040 distinguishable permutations.  We don't need to 
divide by anything because all 7 letters are distinguishable.  

Edwin