SOLUTION: There are 3 parts to this questions. I have been stuck on this question for a long time. PLEASE HELP!! A storage tank contains a radioactive element with a half-life of 6500 yea

Algebra ->  Test -> SOLUTION: There are 3 parts to this questions. I have been stuck on this question for a long time. PLEASE HELP!! A storage tank contains a radioactive element with a half-life of 6500 yea      Log On


   

Question 845641: There are 3 parts to this questions. I have been stuck on this question for a long time. PLEASE HELP!!
A storage tank contains a radioactive element with a half-life of 6500 years. Let f(t) be the percentage of the element that remains at t years since it was placed in the tank.
Question A: Find an equation of f.
Question B: What percentage of the element will remain after 100 years?
Question C: What percentage of the element remains after 26,000 years? [NOTE: this result could be found using the equation of f, but we'll use a different approach to find the percentage].
PLEASE HELP ME SOLVE THIS PROBLEM!!! and PLEASE SHOW WORK SO I CAN UNDERSTAND IT!
Thanks!!
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
A After one half-life the fraction of the element that remains is 1%2F2 .
After 2 half-lives the fraction of the element that remains is 1%2F2 of 1%2F2 , which is %281%2F2%29%2A%281%2F2%29=%281%2F2%29%5E2 .
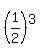After 3 half-lives the fraction of the element that remains is %281%2F2%29%5E3 .
The same idea works for any number of half-lives, even if that number is not an integer.
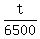t years is t%2F6500 half-lives,
After that time, the fraction of the element that remains is
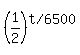
%281%2F2%29%5E%22t+%2F+6500%22
As a percentage, it is f%28t%29=100%2A%281%2F2%29%5E%22t+%2F+6500%22 .
That is an exponential function with base 1%2F2 , and that is not a fashionable base.
Calculators have exponential functions with base 10 and with base e .
The most popular base for exponential functions is the irrational number e .
The reason for that is that calculus works better with e as a base,
so even if you do not intend to ever study calculus, they make you use e rather than 10 .
It is customary to write the function as
f%28t%29=100%2Ae%5E%28%22-+ln+%28+2+%29+%2A+t+%2F+6500%22%29 or f%28t%29=100%2Ae%5E%28%22-+0.693%2At+%2F+6500%22%29 .
It is really the same thing, because the natural logarithm of 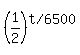%281%2F2%29%5E%22t+%2F+6500%22 is
%28t%2F6500%29%2Aln%281%2F2%29=%28t%2F6500%29%2A%28-ln%282%29%29=-ln%282%29%2At%2F6500 .
People memorize the "formula" for the exponential function with base e without understanding it.
I never memorized that formula, but I can deduce the one with 1%2F2 as a base from the definition of half-life, and then I can "translate" it to base e .

B When t=100 , -0.693%2At%2F6500=-69.3%2F6500 and
f%28t%29=100%2Ae%5E%28%22-69.3+%2F+6500%22%29=100%2A0.989=98.9
So after 100 years 98.9% of the radioactive element remains.

C 26000%2F6500=4 so 26,000 years is 4 half-lives.
The fraction that remains after 4 half-lives is
%281%2F2%29%5E4=1%2F16=0.0625 That is 6.25% .
No formula used. We do not need e for that.