Question 825385: Find all the zeros of the polynomial function.
f(x) = 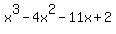
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! As per the rational zero theorem,
the possible rational zeros of  are integers factors of are integers factors of  , meaning , meaning
-2, -1, 1, and 2.
We can try them all, starting by the easiest ones.
Trying 1 and -1 by substitution is easy enough:

 . .
That means that  is not a zero of is not a zero of  , and neither is , and neither is  . .
If  is a zero of is a zero of  , ,  must be a factor of must be a factor of  . If . If  is a zero of is a zero of  , ,  must be a factor of must be a factor of  . .
We could try -2 and 2 by substitution, but since in the end we will need to divide, we may choose just to try dividing by  and by and by  . .
We would find that dividing  by by  leaves a remainder, leaves a remainder,
but that  divides evenly by divides evenly by  , and , and
 . .
That means that  is a zero of is a zero of  , ,
and the remaining zeros are the zeros of  . .
We can use find the zeros of  by solving the quadratic equation by solving the quadratic equation
 either by using the quadratic formula or by "completing the square": either by using the quadratic formula or by "completing the square":




So either  --> -->  , ,
or  --> -->  . .
In sum, the zeros of  are are
 , ,  , and , and  . .
|
|
|