Question 825381: Find all the real zeros of the function.
h(x)= 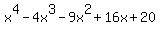
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! As per the rational zero theorem,
the possible rational zeros of 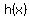 are integers factors of are integers factors of  , meaning , meaning
-20, -5, -4, -2, -1, 1, 2, 4, 5, and 20.
We can try them all, starting by the easiest ones.
Trying 1 and -1, we find  is one zero: is one zero:


Since  is a zero of is a zero of 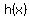 , ,  must be a factor of must be a factor of 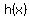 . .
That means that 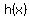 divides evenly by divides evenly by  , with no remainder. , with no remainder.
Dividing 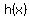 by by  we get we get
 , so , so
 . .
(The division can be done by "synthetic division", or whatever method you have been taught in class).
As per the rational zero theorem,
the possible rational zeros of 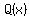 are integers factors of are integers factors of  , meaning , meaning
-20, -5, -4, -2, -1, 1, 2, 4, 5, and 20.
We know that  because otherwise because otherwise 
We can find that  either by substituting 2 for x, either by substituting 2 for x,
or by dividing 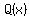 by by  . .
 , ,
and dividing we find that
 . .
So,
 . .
Quadratic polynomial  is easy to factor as is easy to factor as
 , so , so
 . .

and  for for
 , ,  , ,  , and , and  . .
|
|
|