SOLUTION: F(x) = (x+2)/(x+3) where x is not equal to 0. Parentheses are not in the original problem, I included them to show what is over what.

Algebra ->  Test -> SOLUTION: F(x) = (x+2)/(x+3) where x is not equal to 0. Parentheses are not in the original problem, I included them to show what is over what.       Log On


   

Question 778620: F(x) = (x+2)/(x+3) where x is not equal to 0. Parentheses are not in the original problem, I included them to show what is over what.
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
F(x) = (x+2)/(x+3) where x is not equal to 0. Parentheses are not in the original problem, I included them to show what is over what.
I'm glad you put those parentheses there.  Most students would
have written  " x+2/x+3 " which really means 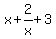x%2B2%2Fx%2B3, an
altogether different expression.

But you didn't state what you were to find.  I assume it is 
the domain and range.

The denominator x+3 must not equal 0, so

x+3 ≠ 0
  x ≠ -3,  so we have a vertical asymptote at x = -3

The degree of the numerator and denominator are both 1, so
the horizontal asymptote is

y = %28LEADING_COEFFICIENT_OF_THE_NUMERATOR%29%2F%28LEADING_COEFFICIENT_OF_THE_DENOMINATOR%29

y = 1%2F1

y = 1 , so we have a horizontal asymptote at y = 1

You also state "x is not equal to 0", so we must leave out the
point (0,2%2F3) and put an open circle there. The two asymptotes
are in green:



So the domain is (-∞,-3)U(-3,0)U(0,∞) and

the range is (-∞,2%2F3)U(2%2F3,1)U(1,∞)

Edwin