Question 701443: How do you find the number of possible x-intercepts and the number of changes in direction?
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! The  of a polynomial are where the polynomial intersects the of a polynomial are where the polynomial intersects the  on the real coordinate plane. Mathematically speaking, these on the real coordinate plane. Mathematically speaking, these  only occur when only occur when  is equal to is equal to  . .
Polynomials can have 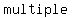 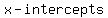 because of the way they curve. The number of because of the way they curve. The number of  a certain polynomial can have is the a certain polynomial can have is the 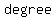 of the polynomial. of the polynomial.
A   polynomial can only have polynomial can only have 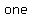 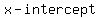 . A . A  degree can have degree can have  to to  , but it doesn't have to have four. For even degree polynomials, it is possible that there are no , but it doesn't have to have four. For even degree polynomials, it is possible that there are no  . .
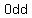 degree polynomials must have degree polynomials must have 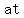 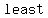  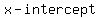 . .
The  are key to graphing a polynomial. They are points that you can connect that lie on the are key to graphing a polynomial. They are points that you can connect that lie on the  . These . These  are also known as are also known as 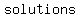 to the to the 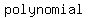 . .
So, how do we find these  ? Simply, these points are where ? Simply, these points are where  . So, you simply solve the polynomial for . So, you simply solve the polynomial for when when  or or  is is  . .
Usually,  cross the cross the  straight through. However, there is more than one way that the polynomial can intercept the straight through. However, there is more than one way that the polynomial can intercept the  . There are actually . There are actually  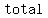 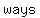 that the graph intercepts the that the graph intercepts the  . In the . In the  , it passes straight through no problem. In the , it passes straight through no problem. In the  , it goes down and touches the , it goes down and touches the  and then rebounds off it. In the and then rebounds off it. In the 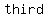 , the graph sort of lingers around the interception point before crossing. , the graph sort of lingers around the interception point before crossing.
Why are there three types of intercepts? This is governed by a mathematical thing called 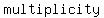 . Multiplicity is the number of times a particular . Multiplicity is the number of times a particular  or solution appears. What if you ended up with the same or solution appears. What if you ended up with the same  twice? That means that that particular twice? That means that that particular  has a multiplicity of has a multiplicity of . It . It 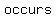 twice, and it therefore has a multiplicity of twice, and it therefore has a multiplicity of  . An . An  that that 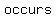  times has a times has a 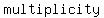 of of  . .
Let us look at the following example:

We could commence the normal procedure for finding  by setting the by setting the  equal to equal to  and solving. However, we end up with and solving. However, we end up with  twice, which means we get the intercept, ( twice, which means we get the intercept, ( , , ), twice. The ), twice. The  , ( , ( , , ) has a multiplicity of ) has a multiplicity of  . .

here are three cases how graph might cross 
1. Normally, an  has a multiplicity of has a multiplicity of 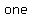 , or it , or it 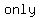 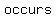 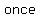 . When this happens, the graph simply passes straight through the . When this happens, the graph simply passes straight through the  . It occurs once, so it passes through and continues along with the normal path that it takes. . It occurs once, so it passes through and continues along with the normal path that it takes.
2. If the intercept has an  multiplicity, meaning it occurs multiplicity, meaning it occurs  , ,  times, times, 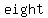 times, etc., then the graph appears to touch the x-axis and then bounces off in the same direction it came from. The graph never passes through the x-axis, it simply touches it and goes back. As multiplicity increases, the valley will become flatter and flatter. times, etc., then the graph appears to touch the x-axis and then bounces off in the same direction it came from. The graph never passes through the x-axis, it simply touches it and goes back. As multiplicity increases, the valley will become flatter and flatter.
3.If the  has an has an  multiplicity, meaning it multiplicity, meaning it 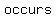 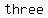 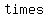 , ,  times, etc., then the graph kind of lingers around the interception point before passing through. The graph does actually pass through, but it is sort of delayed before actually passing through, like in the image. As multiplicity increases, the deflection becomes closer and closer to the times, etc., then the graph kind of lingers around the interception point before passing through. The graph does actually pass through, but it is sort of delayed before actually passing through, like in the image. As multiplicity increases, the deflection becomes closer and closer to the  . .
The graph of a polynomials of degree  , ,  for some constant for some constant  is a is a 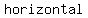 line or line or  is a is a 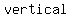 line . It has no turning points and its tails are flat. line . It has no turning points and its tails are flat.
The graph of a polynomial of degree  , ,  ,with ,with 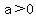 or or 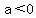 is a slant line with is a slant line with 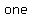 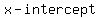 , , 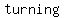 points, and tails in opposite direction. points, and tails in opposite direction.
The graph of a polynomial of degree  . .  with with 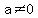 (leading coefficient) is a parabola that opens (leading coefficient) is a parabola that opens  if if 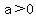 and and  if if 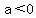 . The graph has . The graph has 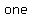 turning point. It can have turning point. It can have  , ,  , or , or   , those that are obtained by shifts, stretching or shrinking and reflections in the , those that are obtained by shifts, stretching or shrinking and reflections in the  negative (or negative (or  negative) axis from negative) axis from  . The function that is not shifted, like . The function that is not shifted, like  , have graphs with tails in opposite directions, one , have graphs with tails in opposite directions, one   and no turning points. They are and no turning points. They are 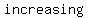 if if 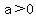 and and 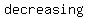 if if 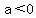 . .

-relative 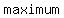 or or  minimum are values where the curve minimum are values where the curve 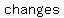 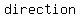
|
|
|