Question 700998: Find any points of discontinuity for the rational function :
(x^3+x^2-4x-4/x^2+2x-3)
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! You probably mean f(x)=(x^3+x^2-4x-4)/(x^2+2x-3) ,
which I can write as
Factoring polynomials never goes away. You have to factor numerator and denominator.
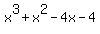 can be factored "by grouping" as
It can be factored further because the difference of squares 
factors as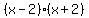 
Putting it all together:
The function is not defined (it does not exist) for  and for  because the denominator is zero for those values of  .
To be continuous, the function has to be defined. So at those points the function is not continuous.
At and at , the function has a vertical asymptote.
As approaches from either side, the denominator approaches zero.
At the same time, the numerator approaches  .
As a consequence the absolute value of the function grows without limits,
and the graph hugs the vertical line .
Something similar happens at .
NOTE: I would call those values of , and , points of discontinuity.
However, names of different kinds of discontinuity are not universally agreed upon,
and some may not like to call and points of discontinuity.
They would say that and are not really points, with an x value and a y value, and the name "points of discontinuity" could be confused with "point discontinuity," which is a different kind of discontinuity.
A function may not be continuous at one point that is just a hole in the graph,
as in  .
That function has  for all values of except  , where g(x) is not defined.
The function graphs as a horizontal line minus the point (-1,1) that is a hole in the graph.
Some call that a "point discontinuity", and others call it a "removable discontinuity".
|
|
|
