SOLUTION: Use compliting square method to write the given quadratic equation y=x^2-2x+3 as y=(x-h)^2+k.

Algebra ->  Test -> SOLUTION: Use compliting square method to write the given quadratic equation y=x^2-2x+3 as y=(x-h)^2+k.      Log On


   

Question 689933: Use compliting square method to write the given quadratic equation
y=x^2-2x+3 as y=(x-h)^2+k.
Answer by MathLover1(20849) About Me  (Show Source):
You can put this solution on YOUR website!

Solved by pluggable solver: Completing the Square to Get a Quadratic into Vertex Form


y=1+x%5E2-2+x%2B3 Start with the given equation



y-3=1+x%5E2-2+x Subtract 3 from both sides



y-3=1%28x%5E2-2x%29 Factor out the leading coefficient 1



Take half of the x coefficient -2 to get -1 (ie %281%2F2%29%28-2%29=-1).


Now square -1 to get 1 (ie %28-1%29%5E2=%28-1%29%28-1%29=1)





y-3=1%28x%5E2-2x%2B1-1%29 Now add and subtract this value inside the parenthesis. Doing both the addition and subtraction of 1 does not change the equation




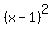
y-3=1%28%28x-1%29%5E2-1%29 Now factor x%5E2-2x%2B1 to get %28x-1%29%5E2



y-3=1%28x-1%29%5E2-1%281%29 Distribute



y-3=1%28x-1%29%5E2-1 Multiply



y=1%28x-1%29%5E2-1%2B3 Now add 3 to both sides to isolate y



y=1%28x-1%29%5E2%2B2 Combine like terms




Now the quadratic is in vertex form y=a%28x-h%29%5E2%2Bk where a=1, h=1, and k=2. Remember (h,k) is the vertex and "a" is the stretch/compression factor.




Check:


Notice if we graph the original equation y=1x%5E2-2x%2B3 we get:


graph%28500%2C500%2C-10%2C10%2C-10%2C10%2C1x%5E2-2x%2B3%29 Graph of y=1x%5E2-2x%2B3. Notice how the vertex is (1,2).



Notice if we graph the final equation y=1%28x-1%29%5E2%2B2 we get:


graph%28500%2C500%2C-10%2C10%2C-10%2C10%2C1%28x-1%29%5E2%2B2%29 Graph of y=1%28x-1%29%5E2%2B2. Notice how the vertex is also (1,2).



So if these two equations were graphed on the same coordinate plane, one would overlap another perfectly. So this visually verifies our answer.