Question 668536: Hi professor I need with synthetic division. 
Thank you!
Found 2 solutions by solver91311, Edwin McCravy:
Answer by solver91311(24713)   (Show Source):
Answer by Edwin McCravy(20055)  (Show Source):
You can put this solution on YOUR website!
This must be considered as
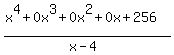Change the sign of the -4 in x-4 to 4.
Start with this:
4 | 1 0 0 0 256
|
Bring down the 1
4 | 1 0 0 0 256
|
1
Multiply the 1 that you just brought down by the 4
at the far left, get 4. Write that 4 just below
the first 0
4 | 1 0 0 0 256
| 4
1
Add the 0 and the 4, get 4, write that at the bottom
like this
4 | 1 0 0 0 256
| 4
1 4
Multiply the 4 that you just wrote down at the bottom
by the 4 at the far left, get 16. Write that 16 just below
the second 0 at the top:
4 | 1 0 0 0 256
| 4 16
1 4
Add the 0 and the 16, get 16, write that at the bottom
like this:
4 | 1 0 0 0 256
| 4 16
1 4 16
Multiply the 16 that you just wrote down at the bottom
by the 4 at the far left, get 64. Write that 64 just below
the third 0 at the top:
4 | 1 0 0 0 256
| 4 16 64
1 4 16
Add the 0 and the 64, get 64, write that at the bottom
like this:
4 | 1 0 0 0 256
| 4 16 64
1 4 16 64
Multiply the 64 that you just wrote down at the bottom
by the 4 at the far left, get 256. Write that 256 just below
the 256 at the top:
4 | 1 0 0 0 256
| 4 16 64 256
1 4 16 64
Add the 256 and the 256, get 512, write that at the bottom
like this:
4 | 1 0 0 0 256
| 4 16 64 256
1 4 16 64 512
Now we interpret the numbers on the bottom line
1. All but the last number are the coefficients of a
polynomial of 1 less degree than the original polynomial.
So the quotient is
1x3 + 4x2 + 16x + 64
and the last number in the bottom of the synthetic
division, 512, is the remainder. Normally we place the
remainder over the divisor, like this:
x3 + 4x2 + 16x + 64 + 
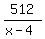Edwin
|
|
|
