Question 647925: What is the slope of a line parallel to the line through the points (8,6) and (-12,-10).
Found 2 solutions by stanbon, MathLover1:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! What is the slope of a line parallel to the line through the points
(8,6) and (-12,-10).
-----
slope = (6--10)/(8--12) = 16/20 = 4/5
=========================================
Cheers,
Stan H.
=============
Answer by MathLover1(20849)  (Show Source):
You can put this solution on YOUR website!
first find the equation of a line through given points (8,6) and (-12,-10).
recall that parallel lines have th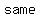e  slope
| Solved by pluggable solver: FIND EQUATION of straight line given 2 points |
hahaWe are trying to find equation of form y=ax+b, where a is slope, and b is intercept, which passes through points (x1, y1) = (8, 6) and (x2, y2) = (-12, -10).
Slope a is  .
Intercept is found from equation  , or  . From that,
intercept b is  , or  .
y=(0.8)x + (-0.4)
Your graph:
|
this line has slope  ; so any other line parallel to this one will have same slope
|
|
|
