SOLUTION: f(x)=(x+1)^3(2x+3)(2-x)^2 determine the degree of f(x) what are the zeros of f(x) help help

Algebra ->  Test -> SOLUTION: f(x)=(x+1)^3(2x+3)(2-x)^2 determine the degree of f(x) what are the zeros of f(x) help help      Log On


   

Question 64288: f(x)=(x+1)^3(2x+3)(2-x)^2
determine the degree of f(x)
what are the zeros of f(x)

help help
Answer by chitra(359) About Me  (Show Source):
You can put this solution on YOUR website!
The given expression is:

f(x) = %28x%2B1%29%5E3+%282x+%2B+3%29%282+-+x%29%5E2

This can be written as:


f(x) = (x+1)(x+1)(x+1)(2x+3)(2-x)(2-x) --------------(EQN 2)

So, on multiplying the given expression it can be writtne as:

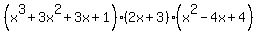
%28x%5E3+%2B+3x%5E2+%2B+3x+%2B+1%29%282x+%2B+3%29%28x%5E2+-+4x+%2B+4%29

This can be simplified and reduced and written as:

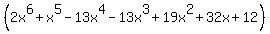
%282x%5E6+%2B+x%5E5+-+13x%5E4+-+13x%5E3+%2B+19x%5E2+%2B+32x+%2B+12%29

Hence, the highest power of x gives us the degree of the polynomial.


The degree of f(x) = 6


Now, the zeros of this one is obtained by:


Equating (2) to zero.

Thus, we find that the zeros of the polynomial are:

x = -1, -1, -1, -2/3, 2, 2


Hence, the solution.

Regards...