Question 614852: the smallest positive zero of the function y=cosk(x+1/2) occurs at x=1/2. find k if k>0
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! The graph of the function y=cos(x) looks like this:
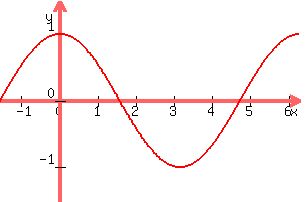
It has a period of  , so it repeats every , and becomes zero again and again at  intervals.
The graph of the function y=cos(x+1/2) looks similar but shifted to the left.  , and the graph looks like this:
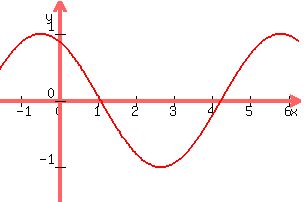
The period is still , so it also repeats every , and it also becomes zero again and again at intervals.
If there is a factor (k) as part of the angle, as in  , the period changes. With a larger k, we cover an angle range of faster and the period gets smaller. For example, y=cos(2x) looks like this:
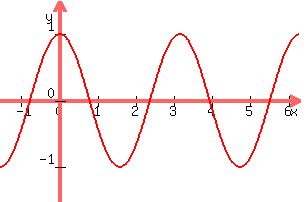
with a period of and zeros at  intervals.
In general the period would be  and the zeros would occur at  intervals.
So if  , the zeros will happen at intervals of  and along with a zero at x=1/2 there would be a smaller positive zero, between x=0 and x=1/2.
The positive k solutions should be 
The most obvious solution is  .
The problem says the smallest positive zero happens for  , and we know that  , so maybe
 --> 
Then, for x=1/2,  , and  ,
but for smaller positive x values,  , the angle 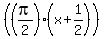 is positive but smaller than , and its cosine is positive, never zero.
Then x=1/2 is the smallest positive zero.
Trial and error could show you that  is also a solution, but we can prove that it is the only other solution.
 -->  for any integer n, and since it must be
, then the only solutions are
and .
|
|
|
