SOLUTION: A certain two digit number Is two more than 3 times the units digit. If the digits if the number are interchanged, the resulting number is 24 less than 4 times the original number.

Algebra ->  Test -> SOLUTION: A certain two digit number Is two more than 3 times the units digit. If the digits if the number are interchanged, the resulting number is 24 less than 4 times the original number.      Log On


   

Question 551145: A certain two digit number Is two more than 3 times the units digit. If the digits if the number are interchanged, the resulting number is 24 less than 4 times the original number. Find the original number. Please help me solve this!!!!!!!
Found 3 solutions by JBarnum, josmiceli, MathTherapy:
Answer by JBarnum(2146) About Me  (Show Source):
You can put this solution on YOUR website!
wow im dizzy just reading this
two digit number will be: ab and ab=10a%2Bb ex:10(1)+2=12
so 10a%2Bb=2%2B3b
interchanged means ba which is 10b%2Ba
so 10b%2Ba=4%2810a%2Bb%29-24
now we have 2 equations solve one equation for 1 variable then use substitution in other equation
10a%2Bb=2%2B3b
10a=2%2B2b
a=%281%2Bb%29%2F5
.
10b%2Ba=4%2810a%2Bb%29-24simplify
10b%2Ba=40a%2B4b-24
6b=39a-24 substitute a
6b=39%28%281%2Bb%29%2F5%29-24distribute 39
6b=%28%2839%2B39b%29%2F5%29-24 multiply all by 5
30b=39%2B39b-120 add like terms
30b=39b-81add 81 and subtract 30b
81=9bdivide
9=b
.
a=%281%2Bb%29%2F5
a=%281%2B9%29%2F5
a=10%2F5
a=2
.
your number is highlight%2829%29
and interchanged is 92 lets check
10a%2Bb=2%2B3b
29=2%2B3%289%29
27=3%289%29
27=27
correct
10b%2Ba=4%2810a%2Bb%29-24
92=4%2829%29-24
92=%28116%29-24
92=92
correct

that was fun got another one? Have a Happy New Year

Answer by josmiceli(19441) About Me  (Show Source):
You can put this solution on YOUR website!
Let +a+ = the 10's digit
Let +b+ = the 1's digit
given:
(1) +10a+%2B+b+=+3b+%2B+2+
(2) +10b+%2B+a+=+4%2A%28+10a+%2B+b+%29+-+24+
---------------------------
(1) +10a+%2B+b+-+3b+=+2+
(1) +10a+-+2b+=+2+
and
(2) +10b+%2B+a+=+40a+%2B+4b+-+24+
(2) +40a+-+a+-+10b+%2B+4b+=+24+
(2) +39a+-+6b+=+24+
-------------------
Multiply both sides of (1) by +3+
and subtract (1) from (2)
(2) +39a+-+6b+=+24+
(1) +-30a+%2B+6b+=+-6+
+9a+=+18+
+a+=+2+
and, since
(1) +10a+-+2b+=+2+
(1) +10%2A2+-+2b+=+2+
(1) +20+-+2b+=+2+
(1) +2b+=+20+-+2+
(1) +2b+=+18+
(1) +b+=+9+
The original number is 29
check:
(2) +10b+%2B+a+=+4%2A%28+10a+%2B+b+%29+-+24+
(2) +10%2A9+%2B+2+=+4%2A%28+10%2A2+%2B+9+%29+-+24+
(2) +92+=+80+%2B+36+-+24+
(2) +92+=+116+-+24+
(2) +92+=+92+
OK

Answer by MathTherapy(10557) About Me  (Show Source):
You can put this solution on YOUR website!

A certain two digit number Is two more than 3 times the units digit. If the digits if the number are interchanged, the resulting number is 24 less than 4 times the original number. Find the original number. Please help me solve this!!!!!!!

Let the tens and units digits be T & U, respectively

Because "A certain two digit number Is two more than 3 times the units digit."

Then:
10T + U = 3U + 2
10T – 2U = 2
5T – U = 1
U = 5T – 1 ---- eq (i)

Because, "the resulting number is 24 less than 4 times the original number," if the digits of the number are interchanged," then:

10U + T = 4(10T + U) – 24
10U + T = 40T + 4U – 24
- 39T + 6U = - 24 ---- eq (ii)

– 39T + 6(5T – 1) = - 24 ------ Substituting 5T – 1 for U in eq (ii)
- 39T + 30T – 6 = - 24
- 9T = - 18
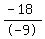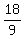T, or tens digit = %28-+18%29%2F-+9, or 18%2F9, or highlight%282%29

U = 5(2) – 1 ----- Substituting 2 for T in eq (i)
U = 10 – 1
U, or units digit = highlight%289%29

Therefore, original number is highlight_green%2829%29

--------
Check
--------
29 = 3(9) + 2 ---- 29 = 27 + 2 ----- 29 = 29 (TRUE)
92 = 4(29) – 24 ----- 92 = 116 – 24 ---- 92 = 92 (TRUE)

Send comments and “thank-yous” to “D” at MathMadEzy@aol.com