Question 463229: If the first and third of three consecutive odd integers are added, the result is 87 less than five times the second integer. Find the third integer.
Answer by MathLover1(20849)   (Show Source):
You can put this solution on YOUR website!
Odd integers are integers that cannot be divided evenly by 2, for example, –5, –3, –1, 1, 3, 5, ... An odd integer always ends in 1, 3, 5, 7, or 9.
Let
the first odd integer is 
the second odd integer is 
the third odd integer is  ..be the three consecutive odd integers (we assume that x>2)
If the first and third of three consecutive odd integers are added,
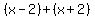
the result is  less than five times the second integer 
so, you have:
 ...........the second odd integer
the first odd integer is 
the third odd integer is 
check:
|
|
|
