Question 427596: when I open a book two page face me. the sum of the page number is 85. what are the page number ? if the sum is not give, but the product is gives to be 1806, how will your find the page number
Found 4 solutions by richard1234, mananth, anmolyadav95170@gmail.com, ikleyn:
Answer by richard1234(7193)   (Show Source):
You can put this solution on YOUR website! We can turn this into an algebra problem by assuming that the integers are x, x+1, x+2, and x+3. Their sum is 178, so
x + (x+1) + (x+2) + (x+3) = 178
4x + 6 = 178
4x = 172, x = 43, so 43, 44, 45, 46 are the integers.
Answer by mananth(16949)  (Show Source):
Answer by anmolyadav95170@gmail.com(1)  (Show Source):
Answer by ikleyn(53354)  (Show Source):
You can put this solution on YOUR website! .
(a) when I open a book two page face me, the sum of the page number is 85. what are the page number ?
(b) if the sum is not give, but the product is gives to be 1806, how will your find the page number
~~~~~~~~~~~~~~~~~~~~~~~
Part (a)
Let the page numbers are n and (n+1), two consecutive integer numbers.
The problem says that
n + (n+1) = 85.
Simplify and find 'n'
2n + 1 = 85,
2n = 85 - n1 = 84,
n = 84/2 = 42.
ANWER. The pages are '42' and '43'.
Part (b)
This time, the equation is
n*(n+1) = 1806.
You can solve it by guessing n = 42 or by advanced guessing with reasoning.
Alternatively, you can reduce it to quadratic equation
n^2 + n - 1806 = 0
and solve it using the quadratic formula or factoring.
Or you can evaluate the square root of 1806: 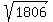 = 42.497 approximately,
which tells you that n = 42.
Thus, both parts, (a) and (b), are solved.
|
|
|
