SOLUTION: I'v etried everything to sole this but for some resason I just can't seem to get it. I would really apperciate some help with this one! Thank you! 135x2 - 222x + 91

Algebra ->  Test -> SOLUTION: I'v etried everything to sole this but for some resason I just can't seem to get it. I would really apperciate some help with this one! Thank you! 135x2 - 222x + 91      Log On


   

Question 35930: I'v etried everything to sole this but for some resason I just can't seem to get it. I would really apperciate some help with this one! Thank you!
135x2 - 222x + 91
Answer by rapaljer(4671) About Me  (Show Source):
You can put this solution on YOUR website!
Wow!! That's a tough one to do by my usual trial and error method. So, let's try setting it equal to zero, and solve by the quadratic formula. The numbers will be HUGE so I'll try to use the Quadratic Equation solver:
135x2+-+222x+%2B+91=+0
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 135x%5E2%2B-222x%2B91+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-222%29%5E2-4%2A135%2A91=144.

Discriminant d=144 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--222%2B-sqrt%28+144+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-222%29%2Bsqrt%28+144+%29%29%2F2%5C135+=+0.866666666666667
x%5B2%5D+=+%28-%28-222%29-sqrt%28+144+%29%29%2F2%5C135+=+0.777777777777778

Quadratic expression 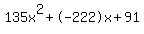135x%5E2%2B-222x%2B91 can be factored:
135x%5E2%2B-222x%2B91+=+%28x-0.866666666666667%29%2A%28x-0.777777777777778%29
Again, the answer is: 0.866666666666667, 0.777777777777778. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+135%2Ax%5E2%2B-222%2Ax%2B91+%29



The solutions are x=0.866666 . . . and x= 0.7777777 . . .
With a calculator you can easily convert these repeating decimals to fractions, and you might be able to get the second one in your head. I get x=13/15, and the second one is x = 7/9.

Now what this means is
x=13/15
15x=13
(15x-13)=0

Also,
x=7/9
9x=7
(9x-7)=0

Therefore the factored form for the trinomial is as follows:
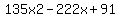
135x2+-+222x+%2B+91
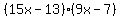
%2815x-13%29%289x-7%29+

My other idea would be to graph this on a graphing calculator that can find the zeros (or roots) of a graph. Determine the decimal values of these roots and convert them to fractions, proceeding in the same way, but without solving by the quadratic formula.

What a GREAT problem! If you want to re-post this question, and see if someone else has any better ideas on it, I will refrain from answering it a second time in order to allow a second opinion. (And I will not have my feelings hurt when I see it posted again!!)

R^2 at SCC