Question 344819: Please help me solve this equation: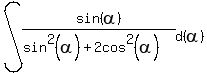 
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! NOTE: To make things easier, I am going to use an "x" instead of  . So whereever you see an "x", read it as
In this form it is not easy to see how to integrate. So we need to start manipulating the expression until we get something we can "see" how to integrate. (As you get more practice with integrals you will develop a better "eye" and "see" how to integrate more and more types of expressions.)
With this one I am going to manipulate the denominator:
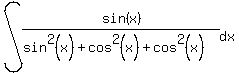
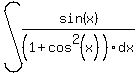
At this point I can see how to proceed. (Eventually you will see this, too.) What I see is a function, cos, with its derivative, sin, in the form:
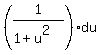
and there is an integration formula for this form. (NOTE: There is a missing minus sign since the derivative of cos is -sin) but missing constant factors can always be "handled".)
So we'll proceed with one more Algebraic adjustment before we use a substitution:
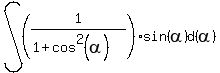
Now we will use a substitution:
The derivative of this:
or
And finally, to match the expression we have in our integrand, we will "move" the minus sign by multiplying both sides by -1:
Now we can make our substitution of u and (-1)du into:
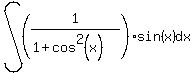
giving:
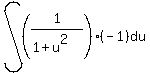
Factoring out the -1 we get:
Now we can use the integration formula for 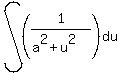 with our "a" being a one. (If you don't recognize this form, you should be able to find it a table of common integration formulas.)
Using the formula we get:
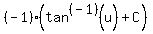
(Note: This is the inverse tangent function. Algebra.com's formula drawing feature does not always handle inverse trig functions well.)
Substituting back in for u and simplifying we get:
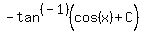
or
-1
-tan (cos(x)) + C
In words the answer is:
(The negative of the inverse tangent of the cosine of alpha) plus the integration constant, C.
|
|
|
