SOLUTION: Find the values of K such that the equation 3x^2 + 10x + K =0 has imaginary roots. I came up with a answer of 25/3 but wasnt sure if that was right

You said you thought the answer is 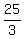.  NO!  There are infinitely
many answers, not just one.  Notice the word "valueS", with an "S", 
not "value". So your answer must be incorrect.  You must
answer with an inequality or with a set in interval notation. 





For the roots to be imaginary this must be negative, which
is the same as less than zero, so we set 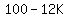 less
than zero.




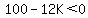
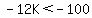
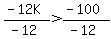
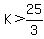 [Note that the inequality reversed because we divided by a negative number] 

The answer is the set of real numbers GREATER THAN .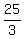
So 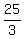 is not even an answer at all, since  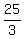is
not greater than itself!!!!

The answer is that K is in the interval   

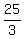
Edwin