SOLUTION: a 13-foot ladder is leaning against a house. the distance from the bottom of the ladder to the house is 7 feet less than the distance from the top of the ladder to the ground. how

Algebra ->  Test -> SOLUTION: a 13-foot ladder is leaning against a house. the distance from the bottom of the ladder to the house is 7 feet less than the distance from the top of the ladder to the ground. how       Log On


   

Question 216520: a 13-foot ladder is leaning against a house. the distance from the bottom of the ladder to the house is 7 feet less than the distance from the top of the ladder to the ground. how far is the bottom of the ladder from the house?
Answer by drj(1380) About Me  (Show Source):
You can put this solution on YOUR website!
A 13-foot ladder is leaning against a house. The distance from the bottom of the ladder to the house is 7 feet less than the distance from the top of the ladder to the ground. How far is the bottom of the ladder from the house?

Step 1. Let c=13 as hypotenuse.

Step 2. Let x be the distance from the top of the ladder to the ground

Step 3. Let y=x-7 be the distance from the bottom of the ladder to the house

Step 4. Use the Pythagorean Theorem which says that the sum of the squares of the legs (x and by)of a right triangle is equal to the sum of the hypotenuse c or x%5E2%2By%5E2=c%5E2

Step 5. Then substitute y of Step 3 into Step 4.


%28x-7%29%5E2%2Bx%5E2=c%5E2=13%5E2

2x%5E2-14x%2B49=169

Subtracting 160 from both sides to get a quadratic equation

2x%5E2-14x%2B49-169=169-169

2x%5E2-14x-120=0

Step 5. The quadratic formula will be used to sole the equation. The formula is given as

x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+

where a=2, b=-14, and c=-120.

Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 2x%5E2%2B-14x%2B-120+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-14%29%5E2-4%2A2%2A-120=1156.

Discriminant d=1156 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--14%2B-sqrt%28+1156+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-14%29%2Bsqrt%28+1156+%29%29%2F2%5C2+=+12
x%5B2%5D+=+%28-%28-14%29-sqrt%28+1156+%29%29%2F2%5C2+=+-5

Quadratic expression 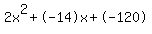2x%5E2%2B-14x%2B-120 can be factored:
2x%5E2%2B-14x%2B-120+=+2%28x-12%29%2A%28x--5%29
Again, the answer is: 12, -5. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+2%2Ax%5E2%2B-14%2Ax%2B-120+%29



Pick the solution, x=12 , since we want positive lengths.

y=x-7=20-7=5

Step 6. ANSWER: The distance from the bottom of the ladder to the house is 5 feet.

I hope the above steps were helpful.

For FREE Step-By-Step videos in Introduction to Algebra, please visit
http://www.FreedomUniversity.TV/courses/IntroAlgebra and for Trigonometry visit
http://www.FreedomUniversity.TV/courses/Trigonometry.

Good luck in your studies!

Respectfully,
Dr J